题目内容
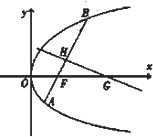 已知点(4,-4)在抛物线C:y2=2px(p>0)上,过焦点F且斜率为k(k>0)的直线交抛物线C于A、B两点,|AB|=8,线段AB的垂直平分线交x轴于点G.
已知点(4,-4)在抛物线C:y2=2px(p>0)上,过焦点F且斜率为k(k>0)的直线交抛物线C于A、B两点,|AB|=8,线段AB的垂直平分线交x轴于点G.(Ⅰ)求抛物线C的标准方程;
(Ⅱ)若线段AB的中点为H,求△FGH的外接圆方程.
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由点(4,-4)在抛物线C:y2=2px(p>0)上,代入计算,可得抛物线C的标准方程;
(Ⅱ)设直线AB的方程为y=k(x-1),代入抛物线方程,确定线段AB的中点H的坐标,△FGH的外接圆即为以FG为直径的圆,即可求△FGH的外接圆方程.
(Ⅱ)设直线AB的方程为y=k(x-1),代入抛物线方程,确定线段AB的中点H的坐标,△FGH的外接圆即为以FG为直径的圆,即可求△FGH的外接圆方程.
解答:
解:(Ⅰ)由已知得,16=2p×4∴p=2
所以抛物线C的标准方程为y2=4x.
(Ⅱ)焦点F(1,0),设直线AB的方程为y=k(x-1),代入抛物线方程,可得k2x-(2k+24)x+k2=0,
设A(x1,y1),B(x2,y2),则x1+x2=
.
∵|AB|=8,∴x1+x2+2=8,
∴
+2=8,
∵k>0,∴k=1.
∵线段AB的中点为H,
∴H(3,2),
∴直线HG的方程为y-2=-(x-3),令y=0得G(5,0),
△FGH的外接圆即为以FG为直径的圆,方程为(x-3)2+y2=4.
所以抛物线C的标准方程为y2=4x.
(Ⅱ)焦点F(1,0),设直线AB的方程为y=k(x-1),代入抛物线方程,可得k2x-(2k+24)x+k2=0,
设A(x1,y1),B(x2,y2),则x1+x2=
| 2k2+4 |
| k2 |
∵|AB|=8,∴x1+x2+2=8,
∴
| 2k2+4 |
| k2 |
∵k>0,∴k=1.
∵线段AB的中点为H,
∴H(3,2),
∴直线HG的方程为y-2=-(x-3),令y=0得G(5,0),
△FGH的外接圆即为以FG为直径的圆,方程为(x-3)2+y2=4.
点评:本题考查抛物线方程,考查圆的方程,考查直线与抛物线的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
观察下列各图,并阅读图形下面的文字,像这样,10条直线相交,交点的个数最多是( )


| A、40 | B、45 | C、50 | D、55 |
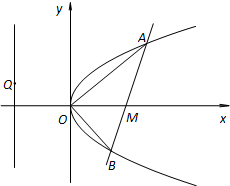 已知直线l过点M(4,0)且与抛物线y2=2px(p>0)交于A、B两点,以弦AB为直径的圆恒过坐标原点O.
已知直线l过点M(4,0)且与抛物线y2=2px(p>0)交于A、B两点,以弦AB为直径的圆恒过坐标原点O.