Question

已知函数f（x）=a（1-|x-1|），a为常数，且a＞1．
（1）求f（x）的最大值；
（2）证明函数f（x）的图象关于直线x=1对称；
（3）当a=2时，讨论方程f（f（x））=m解的个数．

Answer 1

考点：分段函数的应用,函数的最值及其几何意义

专题：函数的性质及应用

分析：对于①去掉绝对值分段讨论；对于②依据对称的定义证明；对于③根据复合函数的定义把绝对值去掉即可

解答： 解：（1）f(x)=a(1-|x-1|)=

a(2-x)，x≥1 ax，x＜1

当x＜1时，f（x）为增函数，最大值为a；当x≥1时，f（x）为减函数，最大值为a，故f（x）的最大值为a．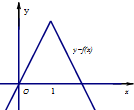
（2）设点（x₀，y₀）为y=f（x）上任意一点，则
，f（2-x₀）=a（1-|2-x₀-1|）=a（1-|1-x₀|）=a（1-|x₀-1|）=y₀=f（x₀）
∴f（2-x₀）=f（x₀），令2-x₀=1+x，则x₀=1-x，∴f（1+x）=f（1-x），即x=1是函数f（x）的对称轴，
所以，函数f（x）的图象关于直线x=1对称．
（3）当a=2时，f(f(x))=

4x，x＜ 1 2 4-4x， 1 2 ≤x＜1 4x-4，1≤x≤ 3 2 8-4x，x＞ 3 2

如图，当m＜0时，方程有2个解；当m=0时，方程有3个解；当0＜m＜2时，方程有4个解；当m=2时，方程有2个解．
综合上述，当m＜0或m=2时，方程有2个解；当m=0时，方程有3个解；当0＜m＜2时，方程有4个解．

点评：本题考查了分段函数单调性，对称的定义，复合函数的性质，综合性较强．