题目内容
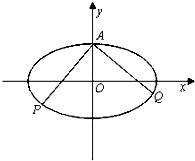 已知左焦点为F1(-2
已知左焦点为F1(-2| 2 |
3
| ||
| 2 |
| ||
| 2 |
(1)求椭圆的标准方程;
(2)若动弦AP所在直线的斜率为1,求直角三角形APQ的面积;
(3)试问动直线PQ是否过定点?若过定点,请给出证明,并求出该定点;若不过定点,请说明理由.
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:解:(1)由题意可设椭圆的标准方程为
+
=1(a>b>0),由题意可得
,解得即可;
(2)由题意可得直线AP的方程为:y=x+1,直线AQ的方程为y=-x+1.分别与椭圆联立解得点P,Q的坐标.利用两点之间的距离公式可得|AP|,|AQ|,再利用三角形的面积计算公式即可得出;
(3)证明:直线PQ过定点M(0,-
).设直线AP的方程为:y=kx+1,则直线AQ的方程为:y=-
x+1.分别与椭圆的方程联立解得点P,Q的坐标.利用斜率计算公式可得kPM=kQM,即可得出P,Q,M三点共线,即可证明.
| x2 |
| a2 |
| y2 |
| b2 |
|
(2)由题意可得直线AP的方程为:y=x+1,直线AQ的方程为y=-x+1.分别与椭圆联立解得点P,Q的坐标.利用两点之间的距离公式可得|AP|,|AQ|,再利用三角形的面积计算公式即可得出;
(3)证明:直线PQ过定点M(0,-
| 4 |
| 5 |
| 1 |
| k |
解答:
解:(1)由题意可设椭圆的标准方程为
+
=1(a>b>0),
由题意可得
,
解得a2=9,b2=1,c=2
.
∴椭圆的方程为
+y2=1.
(2)由题意可得直线AP的方程为:y=x+1,直线AQ的方程为y=-x+1.
联立
,解得
,解得P(-
,-
),
同理解得Q(
,-
).
∴|AP|=|AQ|=
=
,
∴S△APQ=
|AP|2=
×(
)2=
.
(3)证明:直线PQ过定点M(0,-
).
设直线AP的方程为:y=kx+1,则直线AQ的方程为:y=-
x+1.
联立
,化为(1+9k2)x2+18kx=0,
∴xP=
,yP=
,即P(
,
),
同理可得Q(
,
).
∴kPM=
=
,kQM=
=
,
∴kPM=kQM,
∴P,Q,M三点共线.
∴直线PQ过定点M(0,-
).
| x2 |
| a2 |
| y2 |
| b2 |
由题意可得
|
解得a2=9,b2=1,c=2
| 2 |
∴椭圆的方程为
| x2 |
| 9 |
(2)由题意可得直线AP的方程为:y=x+1,直线AQ的方程为y=-x+1.
联立
|
|
| 9 |
| 5 |
| 4 |
| 5 |
同理解得Q(
| 9 |
| 5 |
| 4 |
| 5 |
∴|AP|=|AQ|=
(-
|
9
| ||
| 5 |
∴S△APQ=
| 1 |
| 2 |
| 1 |
| 2 |
9
| ||
| 5 |
| 81 |
| 25 |
(3)证明:直线PQ过定点M(0,-
| 4 |
| 5 |
设直线AP的方程为:y=kx+1,则直线AQ的方程为:y=-
| 1 |
| k |
联立
|
∴xP=
| -18k |
| 1+9k2 |
| 1-9k2 |
| 1+9k2 |
| -18k |
| 1+9k2 |
| 1-9k2 |
| 1+9k2 |
同理可得Q(
| 18k |
| k2+9 |
| k2-9 |
| k2+9 |
∴kPM=
| ||||
-
|
| k2-1 |
| 10k |
| ||||
|
| k2-1 |
| 10k |
∴kPM=kQM,
∴P,Q,M三点共线.
∴直线PQ过定点M(0,-
| 4 |
| 5 |
点评:本题综合考查了椭圆的标准方程及其性质、直线与椭圆的相交问题转化为方程联立可得交点的坐标、两点之间的距离公式、三角形的面积计算公式、斜率计算公式等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
从学号为1~60的高一某班60名学生中随机选取5名同学参加数学测试,采用系统抽样的方法,则所选5名学生的学号可能是( )
| A、10,20,30,40,50 |
| B、6,18,30,42,54 |
| C、2,4,6,8,10 |
| D、4,13,22,31,40 |
观察下列各图,并阅读图形下面的文字,像这样,10条直线相交,交点的个数最多是( )


| A、40 | B、45 | C、50 | D、55 |
下面多面体中有12条棱的是( )
| A、四棱柱 | B、四棱锥 |
| C、五棱锥 | D、五棱柱 |