题目内容
在△ABC中，A=60°，AC=4，BC=2
，则AB等于 ．
| 3 |
考点：余弦定理
专题：解三角形
分析：利用余弦定理列出关系式，把a，b，cosA的值代入求出c的值，即为AB的长．
解答：
解：∵在△ABC中，A=60°，AC=b=4，BC=a=2
，
∴由余弦定理得：a2=b2+c2-2bccosA，即12=16+c2-4c，
解得：c=2，
则AB=c=2，
故答案为：2
| 3 |
∴由余弦定理得：a2=b2+c2-2bccosA，即12=16+c2-4c，
解得：c=2，
则AB=c=2，
故答案为：2
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
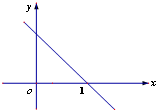函数f（x）的导数f′（x）的图象是如图所示的一条直线l，l与x轴交点坐标为（1，0），则f（0）与f（2）的大小关系为（ ）| A、f（0）＜f（2） |
| B、f（0）＞f（2） |
| C、f（0）=f（2） |
| D、无法确定 |
下列各选项中可以构成集合的是（ ）
| A、相当大的数 |
| B、本班视力较差的学生 |
| C、广州六中2014级学生 |
| D、著名的数学家 |
已知命题p：?x∈R，向量
=（x2，1）与
=（2，1-3x）垂直，则（ ）
| a |
| b |
A、p是假命题；￢p：?x∈R，向量
| ||||
B、p是假命题；￢p：?x∈R，向量
| ||||
C、p是真命题；￢p：?x∈R，向量
| ||||
D、p是真命题；￢p：?x∈R，使得向量
|
设函数f（x）=x2-2|x|-3．