题目内容
函数y=sinx-tanx的图象大致是（ ）
A、 |
B、 |
C、 |
D、 |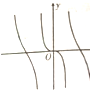
考点：正切函数的图象
专题：三角函数的图像与性质
分析：利用奇偶函数的概念可判断出函数y=sinx-tanx为奇函数，可排除A与B，再利用导数法判断其单调性，即可得到答案．
解答：
解：∵y=sinx与y=tanx均为奇函数，
且f（-x）=sin（-x）-tan（-x）=-（sinx-tanx）=-f（x），
∴y=sinx-tanx为奇函数，
∴函数的图象关于原点对称，可排除A，B；
又y′=cosx-
＜0，
∴y=sinx-tanx在每一个单调区间上均为减函数，可排除C，
故选：D．
且f（-x）=sin（-x）-tan（-x）=-（sinx-tanx）=-f（x），
∴y=sinx-tanx为奇函数，
∴函数的图象关于原点对称，可排除A，B；
又y′=cosx-
| 1 |
| cos2x |
∴y=sinx-tanx在每一个单调区间上均为减函数，可排除C，
故选：D．
点评：本题考查三角函数的图象与性质，着重考查函数的奇偶性与单调性，属于中档题．
练习册系列答案
相关题目
已知向量
，
的夹角为120°，|
|=2，且
•
=-8，则|
|=（ ）
| a |
| b |
| a |
| a |
| b |
| b |
| A、6 | B、7 | C、8 | D、9 |
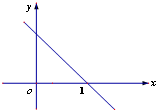函数f（x）的导数f′（x）的图象是如图所示的一条直线l，l与x轴交点坐标为（1，0），则f（0）与f（2）的大小关系为（ ）| A、f（0）＜f（2） |
| B、f（0）＞f（2） |
| C、f（0）=f（2） |
| D、无法确定 |
在△ABC中，内角A，B，C所对应的边分别为a，b，c，若3b=2a，则
的值为（ ）
| sin2A-2sin2B |
| sin2B |
A、-
| ||
B、
| ||
| C、1 | ||
D、
|