题目内容
设a=sin(cos2015°),b=sin(sin2015°),c=cos(sin2015°),d=cos(cos2015°),则( )
| A、d>c>b>a |
| B、d>c>a>b |
| C、c>d>a>b |
| D、c>d>b>a |
考点:复合三角函数的单调性
专题:三角函数的求值
分析:首先,结合诱导公式进行化简,然后,借助于三角函数的单调性进行比较大小即可.
解答:
解:a=sin(cos2015°)=sin(cos215°)=sin(-cos35°)
b=sin(sin2015°)=sin(sin215°)=sin(-sin35°)
c=cos(sin2015°)=cos(sin215°)=cos(-sin35°)=cos(sin35°)
d=cos(cos2015°)=cos(cos215°)=cos(-cos35°)=cos(cos35°)
因sin35°<cos35°,所以0>-sin35°>-cos35°>-1
0>sin(-sin35°)>sin(-cos35°)>-1
因0<sin35°<cos35°<1
所以cos(sin35°)>cos(cos35°)>0
所以sin(-cos35°)<sin(-sin35°)<cos(cos35°)<cos(sin35°)
即a<b<d<c.
故选:D.
b=sin(sin2015°)=sin(sin215°)=sin(-sin35°)
c=cos(sin2015°)=cos(sin215°)=cos(-sin35°)=cos(sin35°)
d=cos(cos2015°)=cos(cos215°)=cos(-cos35°)=cos(cos35°)
因sin35°<cos35°,所以0>-sin35°>-cos35°>-1
0>sin(-sin35°)>sin(-cos35°)>-1
因0<sin35°<cos35°<1
所以cos(sin35°)>cos(cos35°)>0
所以sin(-cos35°)<sin(-sin35°)<cos(cos35°)<cos(sin35°)
即a<b<d<c.
故选:D.
点评:本题重点考查了三角函数诱导公式、三角函数的单调性及其应用,属于中档题.

练习册系列答案
相关题目
若a=log23,b=log32,c=esinπ,则a,b,c 的大小关系为( )
| A、a<b<c |
| B、c<b<a |
| C、a<c<b |
| D、b<c<a |
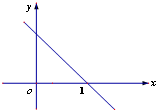 函数f(x)的导数f′(x)的图象是如图所示的一条直线l,l与x轴交点坐标为(1,0),则f(0)与f(2)的大小关系为( )
函数f(x)的导数f′(x)的图象是如图所示的一条直线l,l与x轴交点坐标为(1,0),则f(0)与f(2)的大小关系为( )| A、f(0)<f(2) |
| B、f(0)>f(2) |
| C、f(0)=f(2) |
| D、无法确定 |