题目内容
已知数列{an}中,a1=1,a2=4,a3=12,且{an+1-2an}是等比数列
(1)证明:{
}是等差数列;
(2)求数列{
}的前n项和.
(1)证明:{
| an |
| 2n |
(2)求数列{
| an |
| n |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知得到an+1-2an=2n,两边同时除以2n+1得答案;
(2)由{
}是以
为首项,以
为公差的等差数列求其通项公式,得到数列{
}的通项公式,然后由等比数列的前n项和得答案.
(2)由{
| an |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
| an |
| n |
解答:
(1)证明:∵a1=1,a2=4,a3=12,且{an+1-2an}是等比数列,
∴
=
=
=2,
又a2-2a1=4-2=2,
∴an+1-2an=2n,
则
-
=
.
∴{
}是以
为首项,以
为公差的等差数列;
(2)解:∵{
}是以
为首项,以
为公差的等差数列,
∴
=
+
(n-1)=
,
∴an=
•2n=n•2n-1,
则
=2n-1,
∴数列{
}的前n项和为20+21+22+…+2n-1=
=2n-1.
∴
| an+1-2an |
| an-2an-1 |
| a3-2a2 |
| a2-2a1 |
| 12-8 |
| 4-2 |
又a2-2a1=4-2=2,
∴an+1-2an=2n,
则
| an+1 |
| 2n+1 |
| an |
| 2n |
| 1 |
| 2 |
∴{
| an |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
(2)解:∵{
| an |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| an |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| 2 |
∴an=
| n |
| 2 |
则
| an |
| n |
∴数列{
| an |
| n |
| 1(1-2n) |
| 1-2 |
点评:本题考查了等差关系的确定,考查了等比数列的前n项和,是中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
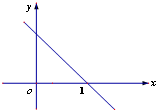 函数f(x)的导数f′(x)的图象是如图所示的一条直线l,l与x轴交点坐标为(1,0),则f(0)与f(2)的大小关系为( )
函数f(x)的导数f′(x)的图象是如图所示的一条直线l,l与x轴交点坐标为(1,0),则f(0)与f(2)的大小关系为( )| A、f(0)<f(2) |
| B、f(0)>f(2) |
| C、f(0)=f(2) |
| D、无法确定 |
在△ABC中,内角A,B,C所对应的边分别为a,b,c,若3b=2a,则
的值为( )
| sin2A-2sin2B |
| sin2B |
A、-
| ||
B、
| ||
| C、1 | ||
D、
|
已知命题p:?x∈R,向量
=(x2,1)与
=(2,1-3x)垂直,则( )
| a |
| b |
A、p是假命题;¬p:?x∈R,向量
| ||||
B、p是假命题;¬p:?x∈R,向量
| ||||
C、p是真命题;¬p:?x∈R,向量
| ||||
D、p是真命题;¬p:?x∈R,使得向量
|