题目内容
已知函数f(x)=
-lnx,其中a∈R,且曲线y=f(x)在点(1,f(1))处的切线垂直于直线y=-x.
(Ⅰ)求a的值;
(Ⅱ)求函数f(x)的单调区间和极值.
| a |
| x |
(Ⅰ)求a的值;
(Ⅱ)求函数f(x)的单调区间和极值.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)求出原函数的导函数,得到函数在x=1时的导数,由f′(1)=-a-1=1求得a的值;
(Ⅱ)把(Ⅰ)中求得的a的值代入函数解析式,求出导函数,得到导函数的零点,判断原函数的单调性,从而求得原函数的极值点并求得极值.
(Ⅱ)把(Ⅰ)中求得的a的值代入函数解析式,求出导函数,得到导函数的零点,判断原函数的单调性,从而求得原函数的极值点并求得极值.
解答:
解:(Ⅰ)∵f(x)=
-lnx,
∴f′(x)=-
-
,
∵曲线y=f(x)在点(1,f(1))处的切线垂直于直线y=-x,
∴f′(1)=-a-1=1,
∴a=-2;
(Ⅱ)由(Ⅰ)知f(x)=-
-lnx,则f′(x)=
-
=
,
令f′(x)=0,解得x=2,
又f(x)的定义域为(0,+∞),
当x∈(0,2)时,f′(x)>0,
∴f(x)在(0,2)内为增函数,
当x∈(2,∞)时,f′(x)<0,
∴f(x)在(2,∞)内为减函数.
由此知函数f(x)在x=2处取得极大值,为f(2)=-1-ln2.
| a |
| x |
∴f′(x)=-
| a |
| x2 |
| 1 |
| x |
∵曲线y=f(x)在点(1,f(1))处的切线垂直于直线y=-x,
∴f′(1)=-a-1=1,
∴a=-2;
(Ⅱ)由(Ⅰ)知f(x)=-
| 2 |
| x |
| 2 |
| x2 |
| 1 |
| x |
| 2-x |
| x2 |
令f′(x)=0,解得x=2,
又f(x)的定义域为(0,+∞),
当x∈(0,2)时,f′(x)>0,
∴f(x)在(0,2)内为增函数,
当x∈(2,∞)时,f′(x)<0,
∴f(x)在(2,∞)内为减函数.
由此知函数f(x)在x=2处取得极大值,为f(2)=-1-ln2.
点评:本题考查了利用导数研究过曲线上某点处的切线方程,过曲线上某点的切线的斜率,就是函数在该点处的导数值,考查了利用导数求函数的极值,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若a=log23,b=log32,c=esinπ,则a,b,c 的大小关系为( )
| A、a<b<c |
| B、c<b<a |
| C、a<c<b |
| D、b<c<a |
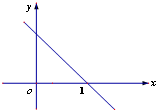 函数f(x)的导数f′(x)的图象是如图所示的一条直线l,l与x轴交点坐标为(1,0),则f(0)与f(2)的大小关系为( )
函数f(x)的导数f′(x)的图象是如图所示的一条直线l,l与x轴交点坐标为(1,0),则f(0)与f(2)的大小关系为( )| A、f(0)<f(2) |
| B、f(0)>f(2) |
| C、f(0)=f(2) |
| D、无法确定 |
设
、
为非零向量,已知命题p:若|
|=2sin
,|
|=4cos
,
•
=1,则
与
的和
;命题q:若函数f(x)=(x
+
)(
-x
)的图象关于y轴对称,则
=
.下列命题正确的是( )
| a |
| b |
| a |
| π |
| 24 |
| b |
| π |
| 24 |
| a |
| b |
| a |
| b |
| π |
| 12 |
| a |
| b |
| a |
| b |
| a |
| b |
| A、p∧q |
| B、p∧(¬q) |
| C、(¬p)∧q |
| D、(¬p)∧(¬q) |
下列各选项中可以构成集合的是( )
| A、相当大的数 |
| B、本班视力较差的学生 |
| C、广州六中2014级学生 |
| D、著名的数学家 |
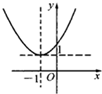

 设函数f(x)=x2-2|x|-3.
设函数f(x)=x2-2|x|-3.