题目内容
已知平面内两定点A（-5，0），B（5，0），动点M满足|MA|-|MB|=10，则点M的轨迹是（ ）
| A、两条射线 | B、双曲线 |
| C、一条射线 | D、双曲线的一支 |
考点：双曲线的定义
专题：圆锥曲线的定义、性质与方程
分析：利用双曲线的定义求解．
解答：
解：平面内两定点A（-5，0），B（5，0），
∵动点M满足|MA|-|MB|=10，
∴点M的轨迹是射线AB．
故选：C．
∵动点M满足|MA|-|MB|=10，
∴点M的轨迹是射线AB．
故选：C．
点评：本题考查点的轨迹的求法，解题时要认真审题，是基础题．
练习册系列答案
相关题目
在△ABC中，已知a=2
，B=30°，b=2，则此三角形（ ）
| 2 |
| A、无解 | B、只有一解 |
| C、有两解 | D、角的个数不确定 |
已知等差数列{an}的公差为2，若a1，a3，a4成等比数列，则a2等于（ ）
| A、-4 | B、-6 | C、-8 | D、-10 |
已知
，
是夹角为60°的两个单位向量，若
=
+
，
=-4
+2
，则
与
的夹角为（ ）
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| a |
| b |
| A、30° | B、60° |
| C、120° | D、150° |
函数y=lg（sinx+cosx）的单调递增区间是（ ）
A、[2kπ-
| ||||
B、（2kπ-
| ||||
C、[2kπ+
| ||||
D、[2kπ+
|
在吸烟与患肺病这两个分类变量的计算中，若从统计量计算中得出有99%的把握说吸烟与患肺病有关的结论，下列说法中正确的是（ ）
| A、若某人吸烟，那么他有99%的可能性患有肺病 |
| B、在100个吸烟者中必有99人患肺病 |
| C、在100个吸烟者中必有1个患肺病 |
| D、所得结论错误的可能性少于1% |
过点P（2，
）作双曲线y=
的切线，则此切线的斜率等于（ ）
| 1 |
| 2 |
| 1 |
| x |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
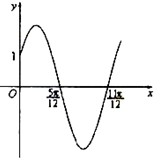已知函数f（x）=Asin（ωx+φ）（x∈R，ω＞0，0＜ω＜| π |
| 2 |
A、f（x）=2sin（2x+
| ||
B、f（x）=2sin（2x+
| ||
C、f（x）=2sin（2x-
| ||
D、f（x）=2sin（2x-
|