题目内容
随机变量X的分布列如下:若E(X)=
,则D(3X+1)的值是 .
| 1 |
| 3 |
| X | -1 | 0 | 1 | ||
| P | a |
| c |
考点:离散型随机变量及其分布列
专题:概率与统计
分析:由题意知:
,由此求出DX,再由D(3X+1)=9D(X)能求出结果.
|
解答:
解:由题意知:
,
解得a=
,c=
,
∴DX=(-1-
)2×
+(0-
)2×
+(1-
)2×
=
,
∴D(3X+1)=9D(X)=5.
故答案为:5.
|
解得a=
| 1 |
| 6 |
| 1 |
| 2 |
∴DX=(-1-
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 9 |
∴D(3X+1)=9D(X)=5.
故答案为:5.
点评:本题考查离散型随机变量的分布列、方差的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
规定a?b=
+2a+b,a、b∈R+,若1?k=4,则函数f(x)=k?x的值域( )
| ab |
| A、(2,+∞) | ||
| B、(1,+∞) | ||
C、[
| ||
D、[
|
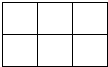 某农场有如图所示的2行3列共六块土地,现有萝卜、玉米、油菜三类蔬菜可种.要求每块土地种一类蔬菜,每类蔬菜种两块土地,每行的蔬菜种类各不相同,则恰有一类蔬菜种在同列的种植方法数为
某农场有如图所示的2行3列共六块土地,现有萝卜、玉米、油菜三类蔬菜可种.要求每块土地种一类蔬菜,每类蔬菜种两块土地,每行的蔬菜种类各不相同,则恰有一类蔬菜种在同列的种植方法数为