题目内容
已知等比数列{an}的各项均为正数，公比q≠1，设P=
（log0.5a4+log0.5a8），Q=log0.5
，则P与Q的大小关系是（ ）
| 1 |
| 2 |
| a2+a10 |
| 2 |
| A、P≥Q | B、P＜Q |
| C、P≤Q | D、P＞Q |
考点：等比数列的性质
专题：等差数列与等比数列
分析：由等比数列的性质化简结合基本不等式可得
＜
，再由对数函数的单调性可得．
| a2•a10 |
| a2+a10 |
| 2 |
解答：
解：由题意可得P=
（log0.5a4+log0.5a8）
=
log0.5（a4•a8）=log0.5
=log0.5
，
由基本不等式可得
≤
，
又公比q≠1，∴a2≠a10，上式取不到等号，
∴
＜
，
又∵对数函数y=log0.5x在（0，+∞）单调递减
∴log0.5
＞log0.5
，
∴P＞Q，
故选：D．
| 1 |
| 2 |
=
| 1 |
| 2 |
| a4•a8 |
=log0.5
| a2•a10 |
由基本不等式可得
| a2•a10 |
| a2+a10 |
| 2 |
又公比q≠1，∴a2≠a10，上式取不到等号，
∴
| a2•a10 |
| a2+a10 |
| 2 |
又∵对数函数y=log0.5x在（0，+∞）单调递减
∴log0.5
| a2•a10 |
| a2+a10 |
| 2 |
∴P＞Q，
故选：D．
点评：本题考查等比数列的性质，涉及基本不等式和对数函数的单调性，属中档题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
观察下面数列的特点，选择适当的数字填入括号中．1，-4，9，-16，25，（ ），49，…
| A、36 | B、±36 |
| C、-36 | D、35 |
若z1=（m2+m+1）+（m2+m-4）i，m∈R，z2=3-2i，则m=1是z1=z2的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
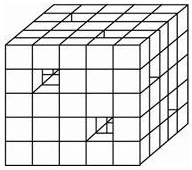如图所示，棱长为6的正方体无论从哪一个面看，都有两个直通的边长为l的正方形孔，则这个有孔正方体的表面积（含孔内各面）是（ ）| A、222 | B、258 |
| C、312 | D、324 |
若
=（1，2），
=（-1，1），
=（2，1），k
+
与
共线，则k的值为（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| A、2 | B、1 | C、0 | D、-1 |
已知⊙O：x2+y2=4，直线l：ax-y+1=0．则直线l与⊙O的位置关系是（ ）
| A、相交 | B、相离 |
| C、相切 | D、与a的值有关 |
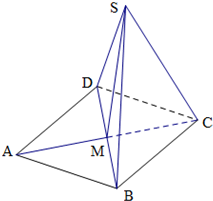菱形ABCD中，∠BAD=60°，AB=4，且AC∩BD=M，现将三角形BD沿着BD折起形成四面体SBCD，如图所示．