题目内容
已知椭圆:
+
=1(a,b>0)和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B.若椭圆上存在点P,使得
•
=0,则椭圆离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| PA |
| PB |
A、[
| ||||||
B、(0,
| ||||||
C、[
| ||||||
D、[
|
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由∠APB=90°及圆的性质,可得|OP|的长,从而可求椭圆的离心率.
解答:
解:由
•
=0,可得∠APB=90°,
利用圆的性质,可得|OP|=
b,
∴|OP|2=2b2≤a2,∴a2≤2c2
∴e2≥
,
∵0<e<1
∴
≤e<1
故选:C.
| PA |
| PB |
利用圆的性质,可得|OP|=
| 2 |
∴|OP|2=2b2≤a2,∴a2≤2c2
∴e2≥
| 1 |
| 2 |
∵0<e<1
∴
| ||
| 2 |
故选:C.
点评:本题考查直线与椭圆的位置关系,考查椭圆的几何性质,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
函数y=2sin(
-2x),x∈[0,π]为增函数的区间是( )
| π |
| 2 |
A、[0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
观察下面数列的特点,选择适当的数字填入括号中.1,-4,9,-16,25,( ),49,…
| A、36 | B、±36 |
| C、-36 | D、35 |
集合A={y|y=
+
},则A的真子集有( )个.
| sinx |
| |sinx| |
| |cosx| |
| cosx |
| A、4 | B、6 | C、7 | D、8 |
等比数列{an}的各项是正数,且a3a11=16,则a7=( )
| A、±4 | B、4 | C、±2 | D、2 |
若z1=(m2+m+1)+(m2+m-4)i,m∈R,z2=3-2i,则m=1是z1=z2的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
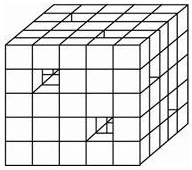 如图所示,棱长为6的正方体无论从哪一个面看,都有两个直通的边长为l的正方形孔,则这个有孔正方体的表面积(含孔内各面)是( )
如图所示,棱长为6的正方体无论从哪一个面看,都有两个直通的边长为l的正方形孔,则这个有孔正方体的表面积(含孔内各面)是( )| A、222 | B、258 |
| C、312 | D、324 |
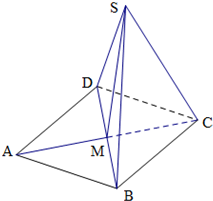 菱形ABCD中,∠BAD=60°,AB=4,且AC∩BD=M,现将三角形BD沿着BD折起形成四面体SBCD,如图所示.
菱形ABCD中,∠BAD=60°,AB=4,且AC∩BD=M,现将三角形BD沿着BD折起形成四面体SBCD,如图所示.