题目内容
某家具厂生产甲、乙两种品牌的组合柜，每种柜制成白坯（成品而未油漆）的工时、油漆工时及有关数据如下表：（利润单位元）
问：该厂每天生产甲、乙这两种组合柜各多少个，才能获得最大的利润？最大利润是多少？
| 产品 时间 工艺要求 |
甲 | 乙 | 能力台时/天 |
| 制白坯时间 | 6 | 12 | 120 |
| 油漆时间 | 8 | 4 | 64 |
| 单位利润 | 200 | 240 |
考点：简单线性规划的应用
专题：应用题,不等式的解法及应用
分析：设生产甲、乙两种型号的组合柜分别为x个、y个，利润为Z元，然后根据题目条件建立约束条件，得到目标函数，画出约束条件所表示的区域，然后利用平移法求出z的最大值，从而求出所求．
解答：
解：设生产甲、乙两种型号的组合柜分别为x个、y个，利润为Z元，
那么
①…（1分）
目标函数为 z=200x+240y…（2分）
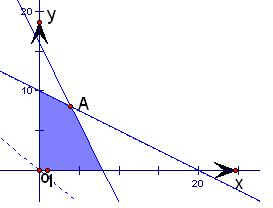
作出二元一次不等式①所表示的平面区域（阴影部分）即可行域．把z=200x+240y变形为y=-
x+
z，得到斜率为-
，在轴上的截距为
z，随z变化的一族平行直线．
如图可以看出，当直线y=-
x+
z经过可行域上M时，截距
z最大，即z最大． …（6分）
解方程组
得A的坐标为x=4，y=8 …（7分）
所以zmax=200x+240y=2720．
答：该公司每天生产生产甲、乙两种型号的组合柜分别为4个、8个，能够产生最大的利润，最大的利润是2720元．
解：设生产甲、乙两种型号的组合柜分别为x个、y个，利润为Z元，那么
|
目标函数为 z=200x+240y…（2分）
作出二元一次不等式①所表示的平面区域（阴影部分）即可行域．把z=200x+240y变形为y=-
| 5 |
| 6 |
| 1 |
| 240 |
| 5 |
| 6 |
| 1 |
| 240 |
如图可以看出，当直线y=-
| 5 |
| 6 |
| 1 |
| 240 |
| 1 |
| 240 |
解方程组
|
得A的坐标为x=4，y=8 …（7分）
所以zmax=200x+240y=2720．
答：该公司每天生产生产甲、乙两种型号的组合柜分别为4个、8个，能够产生最大的利润，最大的利润是2720元．
点评：本题主要考查了简单线性规划的应用，以及平面区域图的画法和二元一次不等式组的解法，属于中档题．
练习册系列答案
相关题目
若z1=（m2+m+1）+（m2+m-4）i，m∈R，z2=3-2i，则m=1是z1=z2的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
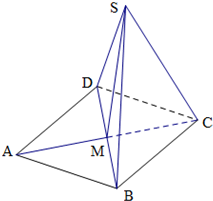菱形ABCD中，∠BAD=60°，AB=4，且AC∩BD=M，现将三角形BD沿着BD折起形成四面体SBCD，如图所示．