题目内容
已知函数f(x)=2
sin
xcos
x+2
cos2
x-
,x∈R.
(1)求函数f(x)的最小正周期、对称中心及取最大值时的x的取值集合;
(2)若函数f(x)图象上的两点P,Q的横坐标依次为2,4,O为坐标原点,求sin∠POQ的值.
| 2 |
| π |
| 8 |
| π |
| 8 |
| 2 |
| π |
| 8 |
| 2 |
(1)求函数f(x)的最小正周期、对称中心及取最大值时的x的取值集合;
(2)若函数f(x)图象上的两点P,Q的横坐标依次为2,4,O为坐标原点,求sin∠POQ的值.
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(1)利用两角和公式和二倍角公式对函数解析式化简整理,利用周期公式求得其最小正周期,根据三角函数图象与性质求得其对称中心和取最大值时,x的集合.
(2)分别求得f(2),f(4),求得P,Q的坐标,|OP|,|PQ|,|OQ|可得,利用向量数量积求得cos∠POQ,则sin∠POQ可求得.
(2)分别求得f(2),f(4),求得P,Q的坐标,|OP|,|PQ|,|OQ|可得,利用向量数量积求得cos∠POQ,则sin∠POQ可求得.
解答:
解:(1)f(x)=2
sin
cos
+
(2cos2
x-1)=
sin
x+
cos
x=2sin(
x+
),
所以,函数f(x)的最小正周期为T=
=8.
由
x+
=kπ(k∈Z)得x=4k-1(k∈Z),
∴函数f(x)的对称中心为(4k-1,0)(k∈Z)
由
x+
=kπ+
(k∈Z)得x=4k+1(k∈Z),
∴函数f(x)的最大值时的x的取值集合{x|x=4k+1}(k∈z),
(2)∵f(2)=2sin(
+
)=2cos
=
,
f(4)=2sin(π+
)=-2sin
=-
,
∴P(2,
),Q(4,-
)
∴|OP|=
,|PQ|=2
,|OQ|=3
从而cos∠POQ=
=
=
∴sin∠POQ=
=
.
| 2 |
| πx |
| 8 |
| πx |
| 8 |
| 2 |
| π |
| 8 |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
所以,函数f(x)的最小正周期为T=
| 2π | ||
|
由
| π |
| 4 |
| π |
| 4 |
∴函数f(x)的对称中心为(4k-1,0)(k∈Z)
由
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
∴函数f(x)的最大值时的x的取值集合{x|x=4k+1}(k∈z),
(2)∵f(2)=2sin(
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
f(4)=2sin(π+
| π |
| 4 |
| π |
| 4 |
| 2 |
∴P(2,
| 2 |
| 2 |
∴|OP|=
| 6 |
| 3 |
| 2 |
从而cos∠POQ=
| ||||
| |OP|•|OQ| |
2×4+
| ||||
|
| ||
| 3 |
∴sin∠POQ=
| 1-cos2∠POQ |
| ||
| 3 |
点评:本题主要考查了三角函数式的化简,三角函数的性质,平面向量数量积的运算.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
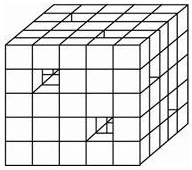 如图所示,棱长为6的正方体无论从哪一个面看,都有两个直通的边长为l的正方形孔,则这个有孔正方体的表面积(含孔内各面)是( )
如图所示,棱长为6的正方体无论从哪一个面看,都有两个直通的边长为l的正方形孔,则这个有孔正方体的表面积(含孔内各面)是( )| A、222 | B、258 |
| C、312 | D、324 |
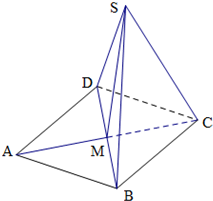 菱形ABCD中,∠BAD=60°,AB=4,且AC∩BD=M,现将三角形BD沿着BD折起形成四面体SBCD,如图所示.
菱形ABCD中,∠BAD=60°,AB=4,且AC∩BD=M,现将三角形BD沿着BD折起形成四面体SBCD,如图所示.