题目内容
已知圆C:(x-1)2+y2=9内有一点P(2,2),过点P作直线l交圆C于A、B两点,
(1)当l经过圆心C时,求直线l的方程;
(2)当弦AB取最小值时,求直线l的方程;
(3)当直线l的倾斜角为45°时,求弦AB的长.
(1)当l经过圆心C时,求直线l的方程;
(2)当弦AB取最小值时,求直线l的方程;
(3)当直线l的倾斜角为45°时,求弦AB的长.
考点:直线与圆的位置关系
专题:直线与圆
分析:(1)由条件利用两点式求得直线l的方程.
(2)当弦AB取最小值时,直线CP和直线l垂直,求得直线l的斜率,再利用点斜式求得直线l的方程.
(3)当直线l的倾斜角为45°时,直线l的斜率为1,由点斜式求得l的方程,再求出圆心到直线l的距离d的值,根据弦长|AB|=2
,计算求得结果.
(2)当弦AB取最小值时,直线CP和直线l垂直,求得直线l的斜率,再利用点斜式求得直线l的方程.
(3)当直线l的倾斜角为45°时,直线l的斜率为1,由点斜式求得l的方程,再求出圆心到直线l的距离d的值,根据弦长|AB|=2
| r2-d2 |
解答:
解:(1)由于圆C:(x-1)2+y2=9的圆心为(1,0),半径r等于3,
当直线l经过点C时,由两点式求得直线l的方程为
=
,化简可得 2x-y-2=0.
(2)当弦AB取最小值时,直线CP和直线l垂直,故直线l的斜率为
=
=-
,
再利用点斜式求得直线l的方程为 y-2=-
(x-2),即 x+2y-6=0.
(3)当直线l的倾斜角为45°时,直线l的斜率为1,方程为y-2=x-2,即 x-y=0,
圆心到直线l的距离d=
=
,∴弦长|AB|=2
=2
=
.
当直线l经过点C时,由两点式求得直线l的方程为
| y-0 |
| 2-0 |
| x-1 |
| 2-1 |
(2)当弦AB取最小值时,直线CP和直线l垂直,故直线l的斜率为
| -1 |
| KCP |
| -1 | ||
|
| 1 |
| 2 |
再利用点斜式求得直线l的方程为 y-2=-
| 1 |
| 2 |
(3)当直线l的倾斜角为45°时,直线l的斜率为1,方程为y-2=x-2,即 x-y=0,
圆心到直线l的距离d=
| 1-0| | ||
|
| ||
| 2 |
| r2-d2 |
9-
|
| 34 |
点评:本题主要考查用两点式、点斜式求直线的方程,点到直线的距离公式,弦长公式的应用,属于基础题.

练习册系列答案
相关题目
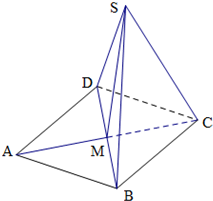 菱形ABCD中,∠BAD=60°,AB=4,且AC∩BD=M,现将三角形BD沿着BD折起形成四面体SBCD,如图所示.
菱形ABCD中,∠BAD=60°,AB=4,且AC∩BD=M,现将三角形BD沿着BD折起形成四面体SBCD,如图所示.