题目内容
16．在底面为正方形的四棱锥S-ABCD中，SA=SB=SC=SD，异面直线AD与SC所成的角为60°，AB=2．则四棱锥S-ABCD的外接球的表面积为（ ）| A． | 6π | B． | 8π | C． | 12π | D． | 16π |
分析 作出直观图，根据所给条件寻找外接球的球心位置，计算球的半径．
解答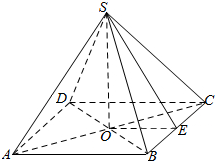 
解：取底面中心O，BC中点E，连结SO，SE，OE，则OE=$\frac{1}{2}AB$=1，OA=OB=OC=OD=$\sqrt{2}$，SO⊥平面ABCD，∴SO⊥OE，
∵AD∥BC，∴∠SCB为异面直线AD，SC所成的角，即∠SCB=60°，
∵SB=SC，∴△SBC是等边三角形，∵BC=AB=2，∴SE=$\sqrt{3}$，∴SO=$\sqrt{S{E}^{2}-O{E}^{2}}$=$\sqrt{2}$．
∴OA=OB=OC=OD=OS，即O为四棱锥S-ABCD的外接球球心．
∴外接球的表面积S=4π×（$\sqrt{2}$）2=8π．
故选：B．
点评 本题考查了球与内接多面体的关系，找出外接球的球心位置是解题关键．
练习册系列答案
相关题目
1．已知sinα=$\frac{\sqrt{3}}{2}$，cosβ=$-\frac{1}{3}$，且tanα•tanβ＞0，则cos（α-β）的值是（ ）
| A． | -$\frac{1-2\sqrt{6}}{6}$ | B． | -$\frac{1+2\sqrt{6}}{6}$ | C． | $\frac{1+2\sqrt{6}}{6}$ | D． | ±$\frac{1+2\sqrt{6}}{6}$ |
5．已知直线y=x+b与两曲线C1：x2+y2-|x|-|y|=0和C2：x2+y2-|x|-|y|=$\frac{1}{2}$仅有两个交点，则实数b的取值范围是（ ）
| A． | （-2，2） | B． | （-1-$\sqrt{2}$，1+$\sqrt{2}$） | C． | （-1-$\sqrt{2}$，-$\sqrt{2}$）∪（-$\sqrt{2}$，1+$\sqrt{2}$） | D． | （-1-$\sqrt{2}$，-2）∪（2，1+$\sqrt{2}$） |
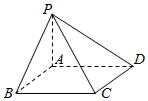如图，四棱锥P-ABCD的底面是边长为4的正方形ABCD，侧棱PA垂直于底面，且PA=3．