题目内容
8.已知四面体各面都是边长为13,14,15的全等三角形.(1)求此三棱锥的体积;
(2)求顶点D到底面的距离.
分析 (1)四面体为长方体切去4个相等的三棱锥得到的,长方体的对角线分别是13,14,15,根据对角线长求出长方体的长宽高;
(2)根据棱锥的体积列出方程解出棱锥的高.
解答 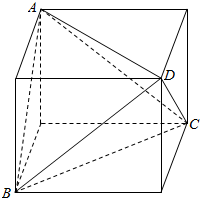 解:(1)∵四面体各面都是边长为13,14,15的全等三角形,
解:(1)∵四面体各面都是边长为13,14,15的全等三角形,
∴该四面体可看做对角线长分别为13,14,15的长方体切去4个相等的三棱锥得到的.设长方体的长宽高分别是a,b,c,
则$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}=1{3}^{2}}\\{{a}^{2}+{c}^{2}=1{4}^{2}}\\{{b}^{2}+{c}^{2}=1{5}^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\sqrt{70}}\\{b=3\sqrt{11}}\\{c=\sqrt{126}}\end{array}\right.$.
∴V=abc-$\frac{1}{3}×\frac{1}{2}abc×4$=$\frac{1}{3}abc$=42$\sqrt{55}$.
(2)cos∠BAC=$\frac{1{3}^{2}+1{4}^{2}-1{5}^{2}}{2×13×14}$=$\frac{5}{13}$,∴sin∠BAC=$\frac{12}{13}$.
∴S△ABC=$\frac{1}{2}×13×14×\frac{12}{13}$=84.设D到底面ABC的距离为h,则$\frac{1}{3}×84h$=42$\sqrt{55}$.解得h=$\frac{3\sqrt{55}}{2}$.
点评 本题考查四面体的体积,顶点A到底面BCD的距离,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
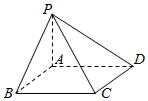 如图,四棱锥P-ABCD的底面是边长为4的正方形ABCD,侧棱PA垂直于底面,且PA=3.
如图,四棱锥P-ABCD的底面是边长为4的正方形ABCD,侧棱PA垂直于底面,且PA=3.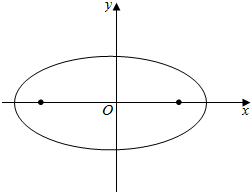 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率 e=$\frac{4}{5}$,且经过点(0,3),左右焦点分别为F1,F2,
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率 e=$\frac{4}{5}$,且经过点(0,3),左右焦点分别为F1,F2,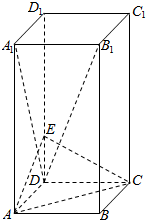 如图,长方体ABCD-A1B1C1D1中,底面ABCD是正方形,AA1=2AB=2,E是DD1上的一点,且满足B1D⊥平面ACE.
如图,长方体ABCD-A1B1C1D1中,底面ABCD是正方形,AA1=2AB=2,E是DD1上的一点,且满足B1D⊥平面ACE.