题目内容
18.一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(2,0,2),(2,2,0),(0,2,2),(1,0,0),画该四面体三视图中的主视图时,以zOx平面为投影面,则得到主视图可以为( )| A. | 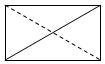 | B. | 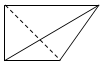 | C. | 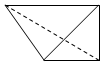 | D. | 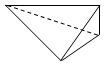 |
分析 由题意,画出直角坐标系,在坐标系中画出几何体,再画出正视图.
解答  解:由题意,画出直角坐标系,
解:由题意,画出直角坐标系,
在坐标系中,画出边长为2的正方体,
则题中各点对应位置如图所示,
以平面zOx为投影面,得到的正视图:
故选:C.
点评 本题考查了空间几何体的三视图;关键要有丰富的空间想象能力,属于中档题.

练习册系列答案
相关题目
1.已知sinα=$\frac{\sqrt{3}}{2}$,cosβ=$-\frac{1}{3}$,且tanα•tanβ>0,则cos(α-β)的值是( )
| A. | -$\frac{1-2\sqrt{6}}{6}$ | B. | -$\frac{1+2\sqrt{6}}{6}$ | C. | $\frac{1+2\sqrt{6}}{6}$ | D. | ±$\frac{1+2\sqrt{6}}{6}$ |
3.已知正三棱锥的正视图和俯视如图所示,则其侧视图的面积为( )
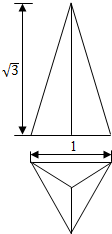

| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
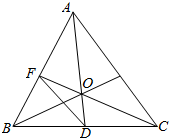 如图所示,已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,$\overrightarrow{OD}$=$\overrightarrow{d}$,$\overrightarrow{OF}$=$\overrightarrow{f}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,$\overrightarrow{f}$表示下列向量.
如图所示,已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,$\overrightarrow{OD}$=$\overrightarrow{d}$,$\overrightarrow{OF}$=$\overrightarrow{f}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,$\overrightarrow{f}$表示下列向量.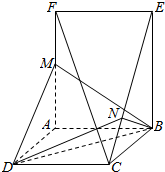 在如图所示的几何体中,正方形ABCD和矩形ABEF所在的平面互相垂直,M为AF上一点,N为CE上一点.
在如图所示的几何体中,正方形ABCD和矩形ABEF所在的平面互相垂直,M为AF上一点,N为CE上一点.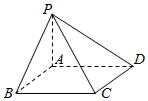 如图,四棱锥P-ABCD的底面是边长为4的正方形ABCD,侧棱PA垂直于底面,且PA=3.
如图,四棱锥P-ABCD的底面是边长为4的正方形ABCD,侧棱PA垂直于底面,且PA=3.