题目内容
圆心在y轴上，半径为1，且过点（1，2）的圆的方程是（ ）
| A、x2+（y-2）2=1 |
| B、x2+（y+2）2=1 |
| C、x2+（y-3）2=1 |
| D、x2+（y+3）2=1 |
考点：圆的标准方程
专题：综合题,直线与圆
分析：设圆心的坐标为（0，b），则由题意可得1=
，解出b，即得圆心坐标，根据半径求得圆的方程．
| 1+(b-2)2 |
解答：
解：设圆心的坐标为（0，b），则由题意可得1=
，∴b=2，
故圆心为（0，2），故所求的圆的方程为 x2+（y-2）2=1．
故选：A．
| 1+(b-2)2 |
故圆心为（0，2），故所求的圆的方程为 x2+（y-2）2=1．
故选：A．
点评：本题考查本题考查圆的标准方程，考查学生的计算能力，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
已知幂函数y=（m2-5m-5）x2m+1在（0，+∞）单调递减，则实数m=（ ）
| A、1 | B、-1 | C、6 | D、-1或6 |
已知函数f（x）=
，则下列结论正确的是（ ）
|
| A、f（x）是偶函数 |
| B、f（x）在f（x）上是增函数 |
| C、f（x）是周期函数 |
| D、f（x）的值域为[-1，+∞） |
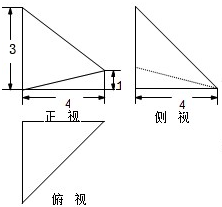已知一个几何体的三视图如图所示，其中正视图是直角梯形．