题目内容
过△OAB的重心G时直线与边OA、OB分别交于P、Q,设
=h•
,
=k
,试证:
+
=3.
| OP |
| OA |
| OQ |
| OB |
| 1 |
| h |
| 1 |
| k |
考点:向量数乘的运算及其几何意义
专题:平面向量及应用
分析:延长OG交边AB与M,则M为AB边中点,可得
=
(
+
)=
(
+
)=
+
.又
=
,代入可得
=
+
.由于P、Q、G三点共线,且
、
是不共线的向量.利用向量共线定理和平面向量基本定理可得
+
=1.
| OM |
| 1 |
| 2 |
| OA |
| OB |
| 1 |
| 2 |
| 1 |
| h |
| OP |
| 1 |
| k |
| OQ |
| 1 |
| 2h |
| OP |
| 1 |
| 2k |
| OQ |
| OM |
| 3 |
| 2 |
| OG |
| OG |
| 1 |
| 3h |
| OP |
| 1 |
| 3k |
| OQ |
| OP |
| OQ |
| 1 |
| 3h |
| 1 |
| 3k |
解答:
证明:延长OG交边AB与M,则M为AB边中点,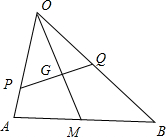
∴
=
(
+
)=
(
+
)=
+
.
又
=
,
∴
=
+
.
∵P、Q、G三点共线,且
、
是不共线的向量.
∴
+
=1,
即
+
=3.

∴
| OM |
| 1 |
| 2 |
| OA |
| OB |
| 1 |
| 2 |
| 1 |
| h |
| OP |
| 1 |
| k |
| OQ |
| 1 |
| 2h |
| OP |
| 1 |
| 2k |
| OQ |
又
| OM |
| 3 |
| 2 |
| OG |
∴
| OG |
| 1 |
| 3h |
| OP |
| 1 |
| 3k |
| OQ |
∵P、Q、G三点共线,且
| OP |
| OQ |
∴
| 1 |
| 3h |
| 1 |
| 3k |
即
| 1 |
| h |
| 1 |
| k |
点评:本题考查了三角形的重心的性质、向量的平行四边形法则、向量共线定理、平面向量基本定理,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目