题目内容
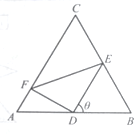 如图,正三角形ABC的边长为2,D、E、F分别在三边AB,BC和CA上,且D为AB的中点,∠EDF=90°,∠BDE=θ(0°<θ<90°).
如图,正三角形ABC的边长为2,D、E、F分别在三边AB,BC和CA上,且D为AB的中点,∠EDF=90°,∠BDE=θ(0°<θ<90°).(1)当tan∠DEF=
| ||
| 2 |
(2)求△DEF的面积S的最小值及使得S取最小值时θ的值.
考点:余弦定理,正弦定理
专题:三角函数的求值
分析:(1)在△BDE中,BD=1,B=60°,∠BED=120°-θ,利用正弦定理表示出DE,在△ADF中,利用正弦定理表示出DF,根据tan∠DEF的值,列表关系式,整理求出tanθ的值,即可确定出θ的大小;
(2)根据两直角边乘积的一半表示出三角形DEF面积S,利用两角和与差的正弦函数公式化简,整理后利用同角三角间基本关系变形,由正弦函数的值域即可确定出S的最小值以及使得S取最小值时θ的值.
(2)根据两直角边乘积的一半表示出三角形DEF面积S,利用两角和与差的正弦函数公式化简,整理后利用同角三角间基本关系变形,由正弦函数的值域即可确定出S的最小值以及使得S取最小值时θ的值.
解答:
解:(1)在△BDE中,由正弦定理
=
得:DE=
=
,
在△ADF中,由正弦定理
=
得:DF=
=
,
∵tan∠DEF=
,
∴
=
,整理得:tanθ=
,
则θ=60°;
(2)S=
DE•DF=
=
=
=
,
当θ=45°时,S取最小值
=
.
| DE |
| sin60° |
| BD |
| sin(120°-θ) |
| BDsin60° |
| sin(120°-θ) |
| ||
| 2sin(60°+θ) |
在△ADF中,由正弦定理
| DF |
| sin60° |
| AD |
| sin(30°+θ) |
| ADsin60° |
| sin(30°+θ) |
| ||
| 2sin(30°+θ) |
∵tan∠DEF=
| ||
| 2 |
∴
| sin(60°+θ) |
| sin(30°+θ) |
| ||
| 2 |
| 3 |
则θ=60°;
(2)S=
| 1 |
| 2 |
| 3 |
| 8sin(60°+θ)sin(30°+θ) |
| 3 | ||||
2(
|
| 3 | ||
2[
|
| 3 | ||
2(
|
当θ=45°时,S取最小值
| 3 | ||
2(
|
6-3
| ||
| 2 |
点评:此题考查了正弦、余弦定理,三角形的面积公式,以及同角三角函数间的基本关系,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
 读该程序图(其中x满足:0<x<12)
读该程序图(其中x满足:0<x<12)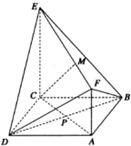 如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,CE=2AF=2
如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,CE=2AF=2