Question

已知线段PQ过△OAB的重心G，且P、Q分别在OA、OB上，设

OA

=

a

，

OB

=

b

，

OP

=m

a

，

OQ

=n

b

，求证：

1

m

+

1

n

=3．

Answer 1

考点：平面向量的基本定理及其意义,平行向量与共线向量

专题：平面向量及应用

分析：由三点P，G，Q共线，可得

OG

=λ

OP

+(1-λ)

OQ

，由重心性质定理可得：

OG

=

2

3

OD

=

2

3

×

1

2

(

OA

+

OB

)=

1

3

(

a

+

b

)，再利用向量基本定理即可得出．

解答： 证明：如图所示，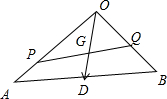
∵三点P，G，Q共线，
∴

OG

=λ

OP

+(1-λ)

OQ

=λm

a

+(1-λ)n

b

，
由重心性质定理可得：

OG

=

2

3

OD

=

2

3

×

1

2

(

OA

+

OB

)=

1

3

(

a

+

b

)，
∴

1

3

a

+

1

3

b

=λm

a

+(1-λ)n

b

，
∴

λm= 1 3 (1-λ)n= 1 3

，
∴

1

m

+

1

n

=3λ+3（1-λ）=3．

点评：本题考查了向量共线定理、重心性质定理、向量基本定理，考查了推理能力与计算能力，属于基础题．