题目内容
已知函数f（x）=-2x
，求f（x）的定义域，并证明f（x）的定义域内，当x1＜x2时，f（x1）＞f（x2）．
| 1 |
| 2 |
考点：函数单调性的判断与证明
专题：计算题,证明题,函数的性质及应用
分析：由偶次根式被开方式非负，可得函数的定义域，再计算f（x1）-f（x2），化简变形和定符号，即可得证．
解答：
解：函数f（x）=-2x
，即为f（x）=-2
，
则定义域为[0，+∞），
证明：令0≤x1＜x2，则f（x1）-f（x2）=-2
+2
=-2（
-
）=-2•
，
由0≤x1＜x2，则x1-x2＜0，
+
＞0，
即有f（x1）-f（x2）＞0，
则f（x1）＞f（x2）．
| 1 |
| 2 |
| x |
则定义域为[0，+∞），
证明：令0≤x1＜x2，则f（x1）-f（x2）=-2
| x1 |
| x2 |
| x1 |
| x2 |
| x1-x2 | ||||
|
由0≤x1＜x2，则x1-x2＜0，
| x1 |
| x2 |
即有f（x1）-f（x2）＞0，
则f（x1）＞f（x2）．
点评：本题考查函数的定义域的求法，考查函数的单调性的证明，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知全集U={0，1，2，3}，A={1，3}，则集合∁UA=（ ）
| A、{0} |
| B、{1，2} |
| C、{0，2} |
| D、{0，1，2} |
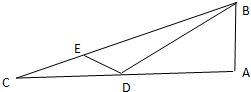如图，在Rt△ABC中，∠A=90°，D是AC上一点，E是BC上一点，若AB=