题目内容
 已知双曲线C1:
已知双曲线C1:| x2 |
| a2 |
| y2 |
| b2 |
(1)求双曲线C1的标准方程;
(2)设F1、F2分别是双曲线C1左、右焦点.若P是该双曲线左支上的一点,且∠F1PF2=60°,求△F1PF2的面积S.
考点:双曲线的简单性质,直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(1)由已知条件设双曲线C1:3x2-y2=λ,λ≠0,把点A(1,0)代入,能求出双曲线C1的标准方程.
(2)设|PF2|=m,|PF1|=n,由已知条件推导出|m-n|=2,由此利用余弦定理能求出mn=12,从而能求出△F1PF2的面积S.
(2)设|PF2|=m,|PF1|=n,由已知条件推导出|m-n|=2,由此利用余弦定理能求出mn=12,从而能求出△F1PF2的面积S.
解答:
解:(1)∵双曲线C1:
-
=1(a>0,b>0)的与双曲线C2:3x2-y2=1有公共渐近线,
∴设双曲线C1:3x2-y2=λ,λ≠0,
∵双曲线C1过点A(1,0),
∴3=λ,∴双曲线C1的标准方程为x2-
=1.
(2)设|PF2|=m,|PF1|=n,
则|m-n|=2,
在△F1PF2中,由余弦定理有16=m2+n2-2mncos60°=|m-n|2+2mn-mn,
∴mn=12,
∴S=
mnsin60°=
×12×
=3
.
| x2 |
| a2 |
| y2 |
| b2 |
∴设双曲线C1:3x2-y2=λ,λ≠0,
∵双曲线C1过点A(1,0),
∴3=λ,∴双曲线C1的标准方程为x2-
| y2 |
| 3 |
(2)设|PF2|=m,|PF1|=n,
则|m-n|=2,
在△F1PF2中,由余弦定理有16=m2+n2-2mncos60°=|m-n|2+2mn-mn,
∴mn=12,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
点评:本题考查双曲线的标准方程的求法,考查三角形面积的求法,是中档题,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
相关题目
若实数x,y满足
,则实数m=
的取值范围是( )
|
| y-1 |
| x+1 |
| A、(-1,1) | ||||
| B、[-1,1) | ||||
C、(-
| ||||
D、[-
|
 已知抛物线C:y2=2px(p>0)的准线方程为x=-2.
已知抛物线C:y2=2px(p>0)的准线方程为x=-2.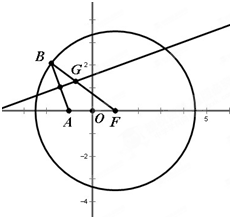 已知:定点A(-1,0),点B是⊙F:(x-1)2+y2=8(F为圆心)上的动点,线段AB的垂直平分线交BF于点G,记点G的轨迹为曲线E.
已知:定点A(-1,0),点B是⊙F:(x-1)2+y2=8(F为圆心)上的动点,线段AB的垂直平分线交BF于点G,记点G的轨迹为曲线E.