题目内容
某车间20名工人年龄数据如下表:
(1)求这20名工人年龄的众数与极差;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)求这20名工人年龄的方差.
| 年龄(岁) | 工人数(人) |
| 19 | 1 |
| 28 | 3 |
| 29 | 3 |
| 30 | 5 |
| 31 | 4 |
| 32 | 3 |
| 40 | 1 |
| 合计 | 20 |
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)求这20名工人年龄的方差.
考点:极差、方差与标准差,茎叶图,众数、中位数、平均数
专题:概率与统计
分析:(1)根据众数和极差的定义,即可得出;
(2)根据画茎叶图的步骤,画图即可;
(3)利用方差的计算公式,代入数据,计算即可.
(2)根据画茎叶图的步骤,画图即可;
(3)利用方差的计算公式,代入数据,计算即可.
解答:
解:(1)这这20名工人年龄的众数为30,极差为40-19=21;
(2)茎叶图如下:

(3)年龄的平均数为:
=30.
这20名工人年龄的方差为S2=
[(19-30)2+3×(28-30)2+3×(29-30)2+5×(30-30)2+4×(31-30)2+3×(32-30)2+(40-30)2]=12.6.
(2)茎叶图如下:

(3)年龄的平均数为:
| 19+28×3+29×3+30×5+31×4+32×3+40 |
| 20 |
这20名工人年龄的方差为S2=
| 1 |
| 20 |
点评:本题考查了众数,极差,茎叶图,方差的基本定义,属于基础题.

练习册系列答案
相关题目
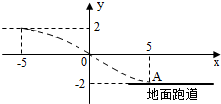 如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( )
如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( )A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=-
|
设命题p:?x∈R,x2+1>0,则¬p为( )
| A、?x0∈R,x02+1>0 |
| B、?x0∈R,x02+1≤0 |
| C、?x0∈R,x02+1<0 |
| D、?x∈R,x2+1≤0 |
若圆C1:x2+y2=1与圆C2:x2+y2-6x-8y+m=0外切,则m=( )
| A、21 | B、19 | C、9 | D、-11 |
 乒乓球台面被网分成甲、乙两部分,如图,甲上有两个不相交的区域A,B,乙被划分为两个不相交的区域C,D,某次测试要求队员接到落点在甲上的来球后向乙回球,规定:回球一次,落点在C上记3分,在D上记1分,其它情况记0分.对落点在A上的来球,小明回球的落点在C上的概率为
乒乓球台面被网分成甲、乙两部分,如图,甲上有两个不相交的区域A,B,乙被划分为两个不相交的区域C,D,某次测试要求队员接到落点在甲上的来球后向乙回球,规定:回球一次,落点在C上记3分,在D上记1分,其它情况记0分.对落点在A上的来球,小明回球的落点在C上的概率为 20名学生某次数学考试成绩(单位:分)的频率分布直方图如图:
20名学生某次数学考试成绩(单位:分)的频率分布直方图如图: