题目内容
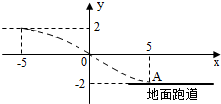 如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( )
如图,某飞行器在4千米高空飞行,从距着陆点A的水平距离10千米处开始下降,已知下降飞行轨迹为某三次函数图象的一部分,则该函数的解析式为( )A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=-
|
考点:导数的几何意义,函数解析式的求解及常用方法
专题:函数的性质及应用,导数的概念及应用
分析:分别求出四个选项中的导数,验证在x=±5处的导数为0成立与否,即可得出函数的解析式.
解答:
解:由题意可得出,此三次函数在x=±5处的导数为0,依次特征寻找正确选项:
A选项,导数为y′=
x2-
,令其为0,解得x=±5,故A正确;
B选项,导数为y′=
x2-
,令其为0,x=±5不成立,故B错误;
C选项,导数为y′=
x2-1,令其为0,x=±5不成立,故C错误;
D选项,导数为y′=-
x2+
,令其为0,x=±5不成立,故D错误.
故选:A.
A选项,导数为y′=
| 3 |
| 125 |
| 3 |
| 5 |
B选项,导数为y′=
| 6 |
| 125 |
| 4 |
| 5 |
C选项,导数为y′=
| 9 |
| 125 |
D选项,导数为y′=-
| 9 |
| 125 |
| 1 |
| 5 |
故选:A.
点评:本题考查导数的几何意义,导数几何意义是导数的重要应用.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=cos(2x+
)的最小正周期是( )
| π |
| 4 |
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
已知f(x)为偶函数,当x≥0时,f(x)=
,则不等式f(x-1)≤
的解集为( )
|
| 1 |
| 2 |
A、[
| ||||||||
B、[-
| ||||||||
C、[
| ||||||||
D、[-
|
 底面边长为2的正三棱锥P-ABC,其表面展开图是三角形P1P2P3,如图,求△P1P2P3的各边长及此三棱锥的体积V.
底面边长为2的正三棱锥P-ABC,其表面展开图是三角形P1P2P3,如图,求△P1P2P3的各边长及此三棱锥的体积V.