题目内容
y=|ax-1|和y=(a-1)x没有交点,则a的取值范围是 .
考点:函数的图象
专题:函数的性质及应用
分析:根据函数的零点,需要分类讨论,(1)当a=1时,(2)当a=0时,(3)当a>0,且a≠1时,(4)当a<0时,分别对每一种情况分析即可
解答:
解:∵y1=|ax-1|和y2=(a-1)x没有交点,
∴y1的零点为
,y2的零点为0,交点情况讨论如下
(1)当a=1时,y2的图象为x轴,如下图所示显然不合题意,舍去,
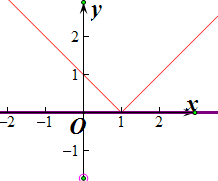
(2)当a=0时,解得x=-1,两图象有公共点,如下图所示显然不合题意,舍去,
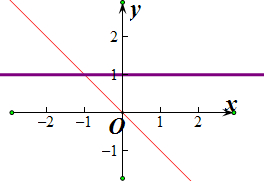
(3)当a>0,且a≠1时,要使两图象没有交点只需要满足,
a-1≥-a,且a-1<0,解得
≤a<1
如图所示
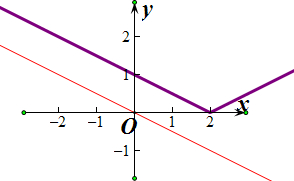
(4)当a<0时,由图可知,两图象不可能没有交点,舍去
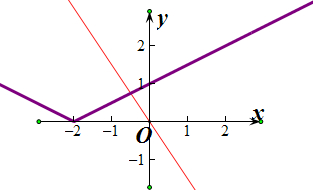
综上所述:a的取值范围是[
,1),
故答案为:[
,1),
∴y1的零点为
| 1 |
| a |
(1)当a=1时,y2的图象为x轴,如下图所示显然不合题意,舍去,

(2)当a=0时,解得x=-1,两图象有公共点,如下图所示显然不合题意,舍去,
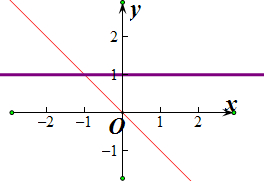
(3)当a>0,且a≠1时,要使两图象没有交点只需要满足,
a-1≥-a,且a-1<0,解得
| 1 |
| 2 |
如图所示
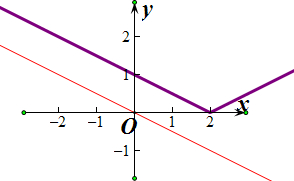
(4)当a<0时,由图可知,两图象不可能没有交点,舍去

综上所述:a的取值范围是[
| 1 |
| 2 |
故答案为:[
| 1 |
| 2 |
点评:本题主要考查了函数的交点问题,需要分类讨论,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
集合M={(x,y)|x=
},N={(x,y)|y=x+m},若M∩N的子集恰有4个,则M的取值范围是( )
| 1-y2 |
A、[-
| ||||
B、[1,
| ||||
C、[-1,
| ||||
D、(-
|
设函数f(x)=
(a>0,x∈R),已知区间A=[
,
](m<n),集合B={f(x)|m≤x≤n},则使得A=B成立的实数a的取值范围是( )
| 2ax3 |
| 1+|x| |
| m2 |
| 2 |
| n2 |
| 2 |
A、a>
| ||
B、a≤
| ||
C、0<a≤
| ||
D、0<a<
|
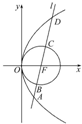 如图,抛物线C1:y2=4x和圆C2:(x-1)2+y2=1,直线l经过C1的焦点F,依次交C1,C2于A,B,C,D四点,则
如图,抛物线C1:y2=4x和圆C2:(x-1)2+y2=1,直线l经过C1的焦点F,依次交C1,C2于A,B,C,D四点,则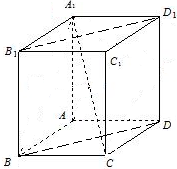 已知长方体A1B1C1D1-ABCD的高为
已知长方体A1B1C1D1-ABCD的高为