题目内容
17.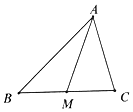 如图,锐角△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点M为BC的中点.
如图,锐角△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点M为BC的中点.(Ⅰ)试用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{AM}$;
(Ⅱ)若|$\overrightarrow{a}$|=5,|$\overrightarrow{b}$|=3,sin∠BAC=$\frac{4}{5}$,求中线AM的长.
分析 (Ⅰ)根据向量的加法以及中点的定义求出$\overrightarrow{AM}$即可;
(Ⅱ)求出∠BAC的余弦值,从而求出AM的长即可.
解答 解:(Ⅰ)∵M是BC的中点
∴$\overrightarrow{AM}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$);
(Ⅱ)∵sin∠BAC=$\frac{4}{5}$,△ABC是锐角三角形,
∴cos∠BAC=$\frac{3}{5}$,
∴${|\overrightarrow{AM}|}^{2}$=$\frac{1}{4}$(${\overrightarrow{a}}^{2}$+2$\overrightarrow{a}$•$\overrightarrow{b}$+${\overrightarrow{b}}^{2}$)=$\frac{1}{4}$(25+2×5×3×$\frac{3}{5}$+9)=13,
∴|$\overrightarrow{AM}$|=$\sqrt{13}$,即中线AM=$\sqrt{13}$.
点评 本题考查平面向量基本定理,模的几何意义,简单题.

练习册系列答案
相关题目
5.已知直线l的参数方程为:$\left\{\begin{array}{l}{x=2t}\\{y=1+4t}\end{array}\right.$(t为参数),圆C的极坐标方程为$ρ=2\sqrt{2}sinθ$,则直线l与圆C的位置关系为( )
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 无法确定 |
7.4名同学甲、乙、丙、丁按任意次序站成一排,甲或乙站在边上的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{6}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
4.某小组有7人,现在从任选3人相互调整位置,其余4人位置不变,则不同调整方案有( )种.
| A. | 35 | B. | 70 | C. | 210 | D. | 105 |
 如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,平面PCD⊥平面ABCD,M是PB的中点,且∠BCD=120°.
如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,平面PCD⊥平面ABCD,M是PB的中点,且∠BCD=120°. 某货运公司规定,从甲城到乙城的计价标准是:40吨以内100元(含40吨),超出40吨的部分4元/吨.
某货运公司规定,从甲城到乙城的计价标准是:40吨以内100元(含40吨),超出40吨的部分4元/吨.