题目内容
5.设函数f(x)为R上的奇函数,已知当x>0时,f(x)=-(x+1)2.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若f(m2+2m)+f(m)>0,求m的取值范围.
分析 (Ⅰ)根据函数奇偶性的性质进行转化求解即可.
(Ⅱ)根据条件判断函数的单调性,利用函数奇偶性和单调性的关系进行转化求解即可.
解答 解:(Ⅰ)∵函数f(x)为R上的奇函数,
∴f(0)=0,
若x<0,则-x>0,
∵当x>0时,f(x)=-(x+1)2.
∴当-x>0时,f(-x)=-(-x+1)2=-(x-1)2.
∵f(x)是奇函数,
∴f(-x)=-(x-1)2=-f(x),
则f(x)=(x-1)2,x<0,
则函数f(x)的解析式f(x)=$\left\{\begin{array}{l}{(x-1)^{2},}&{x<0}\\{0,}&{x=0}\\{-(x+1)^{2},}&{x>0}\end{array}\right.$;
(Ⅱ)若f(m2+2m)+f(m)>0,
则f(m2+2m)>-f(m)=f(-m),
当x>0时,f(x)=-(x+1)2为减函数,且f(x)<-1<f(0),
当x<0时,f(x)=(x-1)2为减函数,且f(x)>1>f(0),
则函数f(x)在R上是减函数,
则m2+2m<-m,
即m2+3m<0,
则-3<m<0,
即m的取值范围是(-3,0).
点评 本题主要考查函数解析式的求解,利用函数函数单调性和奇偶性的关系将不等式进行转化求解是解决本题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
15.已知函数$f(x)=1+x-\frac{x^2}{2}+\frac{x^3}{3}-…+\frac{{{x^{2017}}}}{2017}$,设F(x)=f(x+4),且F(x)的零点均在区间(a,b)内,其中a,b∈Z,a<b,则F(x)>0的最小整数解为( )
| A. | -1 | B. | 0 | C. | -5 | D. | -4 |
16.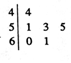 为了检查某高三毕业班学生的体重情况,从该班随机抽取了6位学生进行称重,如图为6位学生体重的茎叶图(单位:kg),其中图中左边是体重的十位数字,右边是个位数字,则这6位学生体重的平均数为( )
为了检查某高三毕业班学生的体重情况,从该班随机抽取了6位学生进行称重,如图为6位学生体重的茎叶图(单位:kg),其中图中左边是体重的十位数字,右边是个位数字,则这6位学生体重的平均数为( )
 为了检查某高三毕业班学生的体重情况,从该班随机抽取了6位学生进行称重,如图为6位学生体重的茎叶图(单位:kg),其中图中左边是体重的十位数字,右边是个位数字,则这6位学生体重的平均数为( )
为了检查某高三毕业班学生的体重情况,从该班随机抽取了6位学生进行称重,如图为6位学生体重的茎叶图(单位:kg),其中图中左边是体重的十位数字,右边是个位数字,则这6位学生体重的平均数为( )| A. | 52 | B. | 53 | C. | 54 | D. | 55 |
13.下列函数中是奇函数的是( )
| A. | y=x+sinx | B. | y=|x|-cosx | C. | y=xsinx | D. | y=|x|cosx |
10.下列函数在其定义域上既是奇函数又是减函数的是( )
| A. | f(x)=2x | B. | f(x)=log${\;}_{\frac{1}{2}}$x | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=-x|x| |
14.下列各组中的函数f(x),g(x)表示同一函数的是( )
| A. | f(x)=x,g(x)=${(\sqrt{x}\;)^2}$ | B. | f(x)=x+1,g(x)=$\frac{{{x^2}-1}}{x-1}$ | ||
| C. | f(x)=|x|,g(x)=$\sqrt{{x}^{2}}$ | D. | f(x)=log22x,g(x)=2log2x |
15.已知函数$f(x)=\left\{{\begin{array}{l}{1-|x|,x≤1}\\{{{({x-1})}^2},x>1}\end{array}}\right.$,若方程f(1-x)-m=0有三个不相等的实数根,则实数m的取值范围为( )
| A. | (-∞,1) | B. | $({\frac{3}{4},+∞})$ | C. | (0,2) | D. | (0,1) |