题目内容
20.函数f(x)=2cos2x•tanx+cos2x的最小正周期为π;最大值为$\sqrt{2}$.分析 利用三角函数的恒等变换化简函数的解析式,再利用正弦函数的周期性以及最大值得出结论.
解答 解:函数f(x)=2cos2x•tanx+cos2x=2sinxcosx+cos2x=sin2x+cos2x
=$\sqrt{2}$sin(2x+$\frac{π}{4}$)的最小正周期为$\frac{2π}{2}$=π,最大值为$\sqrt{2}$,
故答案为:π,$\sqrt{2}$
点评 本题主要考查三角函数的恒等变换,正弦函数的周期性以及最大值,属于基础题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
10.若集合M⊆N,则以下集合中一定是空集的是( )
| A. | M∩N | B. | M∩∁UN | C. | ∁UM∩N | D. | M∪N |
15.函数f(x)=log2x+x-4的零点在区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
12.已知直线l1的方程为Ax+3y+C=0,直线l2的方程为2x-3y+4=0,若l1与l2的交点在y轴上,则C的值为( )
| A. | 4 | B. | -4 | C. | ±4 | D. | 与A有关 |
10.已知某几何体的三视图如图,则该几何体的体积是( )
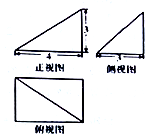

| A. | 48 | B. | 36 | C. | 24 | D. | 12 |
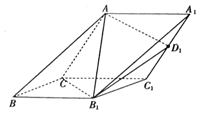 如图,在三棱柱ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2$\sqrt{3}$.
如图,在三棱柱ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2$\sqrt{3}$.