题目内容
15.已知函数$f(x)=\left\{{\begin{array}{l}{1-|x|,x≤1}\\{{{({x-1})}^2},x>1}\end{array}}\right.$,若方程f(1-x)-m=0有三个不相等的实数根,则实数m的取值范围为( )| A. | (-∞,1) | B. | $({\frac{3}{4},+∞})$ | C. | (0,2) | D. | (0,1) |
分析 由题意可得f(1-x)=m有三个不相等的实数根,作出y=f(1-x)的图象和直线y=m,通过图象观察,即可得到m的范围.
解答  解:方程f(1-x)-m=0有三个不相等的实数根,
解:方程f(1-x)-m=0有三个不相等的实数根,
即为f(1-x)=m有三个不相等的实数根,
作出y=f(1-x)的图象和直线y=m,
y=f(1-x)的图象可看作是由y=f(x)的图象先关于y轴对称,
再向右平移1个单位得到.
通过图象可得当0<m<1时,函数y=f(1-x)和直线y=m有3个交点,
即为方程f(1-x)-m=0有三个不相等的实数根.
故选:D.
点评 本题考查函数方程的转化思想,考查数形结合的思想方法,以及图象平移,属于中档题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
10.已知某几何体的三视图如图,则该几何体的体积是( )
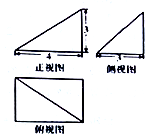

| A. | 48 | B. | 36 | C. | 24 | D. | 12 |
7.已知命题p:?x∈R,$sinx>\frac{{\sqrt{3}}}{2}$,则( )
| A. | ﹁p:?x∈R,sin $x≤\frac{{\sqrt{3}}}{2}$ | B. | ﹁p:?x∈R,$sinx<\frac{{\sqrt{3}}}{2}$ | ||
| C. | ﹁p:?x∈R | D. | ﹁p:?x∈R,$sinx≤\frac{{\sqrt{3}}}{2}$ |
4.执行如图所示的程序框图,则输出的 a=( )


| A. | 1 | B. | -1 | C. | -4 | D. | $-\frac{5}{2}$ |
5.方程log2x+x=3的解所在区间是( )
| A. | (0,1) | B. | (1,2) | C. | (3,+∞) | D. | [2,3) |
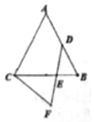 如图,△ABC为边长为1的正三角形,D为AB的中点,E在BC上,且BE:EC=1:2,连结DE并延长至F,使EF=DE,连结FC,则$\overrightarrow{FC}$•$\overrightarrow{AC}$的值为$\frac{7}{12}$.
如图,△ABC为边长为1的正三角形,D为AB的中点,E在BC上,且BE:EC=1:2,连结DE并延长至F,使EF=DE,连结FC,则$\overrightarrow{FC}$•$\overrightarrow{AC}$的值为$\frac{7}{12}$.