下列函数在其定义域上既是奇函数又是减函数的是( )A．f(x)=2xB．f(x)=log${\;} {\frac{1}{2}}$xC．f(x)=$\frac{1}{x}$D．f(x)=-x|x| 题目和参考答案——青夏教育精英家教网——

题目内容

10．下列函数在其定义域上既是奇函数又是减函数的是（　　）

A．

f（x）=2^x

B．

f（x）=log${\;}_{\frac{1}{2}}$x

C．

f（x）=$\frac{1}{x}$

D．

f（x）=-x|x|

分析利用奇偶性、单调性的定义，分别进行判断，即可得出结论．

解答解：对于A，B，非奇非偶函数；
对于C，是奇函数，不是定义域上的减函数；
对于D，在其定义域上既是奇函数又是减函数，
故选：D．

点评本题考查函数奇偶性、单调性的定义，考查学生对概念的理解，属于中档题．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

20．已知f（x）=$\left\{\begin{array}{l}{{2}^{x-1}（x≥1）}\\{3x-2（x＜1）}\end{array}\right.$，若对任意θ∈[0，$\frac{π}{2}$]，不等式f（cos²θ+λsinθ-$\frac{1}{3}$）+$\frac{1}{2}$＞0恒成立，整数λ的最小值为1．

1．已知条件p：k-2≤x-2≤k+2，条件q：1＜2^x＜32，若p是q的充分不必要条件，求实数k的取值范围．

18．设函数f（x）=$\left\{\begin{array}{l}{{2}^{x}，x≤0}\\{lo{g}_{0.5}x，x＞0}\end{array}\right.$，则下列说法正确的是（　　）
①若a≤0，则f（f（a））=-a；
②若f（f（a））=-a，则a≤0；
③若a≥1，则f（f（a））=$\frac{1}{a}$；
④若f（f（a））=$\frac{1}{a}$，则a≥1．

5．设函数f（x）为R上的奇函数，已知当x＞0时，f（x）=-（x+1）²．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若f（m²+2m）+f（m）＞0，求m的取值范围．

15．已知三棱柱ABC-A₁B₁C₁的侧棱垂直于底面，各顶点都在同一球面上，若该棱柱的体积为$\sqrt{3}$，BC=$\sqrt{3}$，AC=1，∠ACB=90°，则此球的体积等于（　　）

$\frac{40\sqrt{10}}{3}$π

$\frac{64\sqrt{2}}{3}$π

$\frac{8\sqrt{2}}{3}$π

2．在△ABC中，点M是BC的中点，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，则$\overrightarrow{AM}$=（　　）

$\overrightarrow{a}$+$\overrightarrow{b}$

$\overrightarrow{a}$-$\overrightarrow{b}$

$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$

$\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$

19．设f（x）是R上的偶函数，且在[0，+∞）上是单调递增，若f（2）=0，则使f（log${\;}_{\frac{1}{2}}$x）＜0成立的x的取值范围是（　　）

（$\frac{\sqrt{2}}{2}$，4）

（0，$\frac{1}{4}$）

（$\frac{1}{4}$，$\frac{\sqrt{2}}{2}$）

（$\frac{1}{4}$，4）

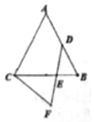如图，△ABC为边长为1的正三角形，D为AB的中点，E在BC上，且BE：EC=1：2，连结DE并延长至F，使EF=DE，连结FC，则$\overrightarrow{FC}$•$\overrightarrow{AC}$的值为$\frac{7}{12}$．