题目内容
设集合A=|f（x）|存在互不相等的正整数m，n，k，使得[f（n）]2=f（m）f（k），则不属于集合A的函数是（ ）
| A、f（x）=2x-1 |
| B、f（x）=x2 |
| C、f（x）=2x+1 |
| D、f（x）=log2x |
考点：函数的值
专题：函数的性质及应用
分析：根据条件分别确定n，m，k的值即可得到结论．
解答：
解：A．∵f（1）=1，f（2）=3，f（5）=9，∴满足[f（2）]2=f（1）f（5）．
B．∵f（1）=1，f（2）=4，f（4）=16，∴满足[f（2）]2=f（1）f（4）．
D..∵f（2）=1，f（4）=2，f（16）=4，∴满足[f（4）]2=f（2）f（16）．
故只有C不满足条件．
故选：C．
B．∵f（1）=1，f（2）=4，f（4）=16，∴满足[f（2）]2=f（1）f（4）．
D..∵f（2）=1，f（4）=2，f（16）=4，∴满足[f（4）]2=f（2）f（16）．
故只有C不满足条件．
故选：C．
点评：本题主要考查函数值的计算，根据条件找出满足条件的n，m，k是解决本题的关键，比较基础．
练习册系列答案
相关题目
已知函数f（x）=2x+x，g（x）=log3x+x，h（x）=x-
的零点依次为a，b，c，则（ ）
| 1 | ||
|
| A、a＜b＜c |
| B、c＜b＜a |
| C、c＜a＜b |
| D、b＜a＜c |
“函数y=sin（x+φ）为偶函数”是“φ=
”的（ ）
| π |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
各项均为实数的等比数列{an}中，a1=1，a5=4，则a3=（ ）
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
在平面直角坐标系中，x轴的正半轴上有4个点，y轴的正半轴上有5个点，这9个点任意两点连线，则所有连线段的交点落入第一象限的个数最多是（ ）
| A、30 | B、60 |
| C、120 | D、240 |
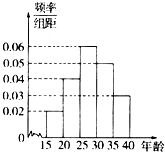山东省第二十三届运动会将于2014年9月16日在济宁市开幕，为办好省运会，济宁市计划招募各类志愿者1.2万人．为做好宣传工作，招募小组对济宁市15-40岁的人群随机抽取了100人，回答“省运会”的有关知识，根据统计结果制作了如下的统计图及表：
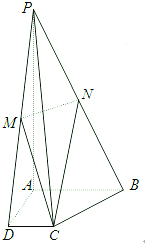如图，四棱锥P-ABCD，PA⊥平面ABCD，且PA=4，底面ABCD为直角梯形，∠CDA=∠BAD=90°，AB=2，CD=1，