题目内容
已知函数f(x)=ln|x+1|-ax2.
(Ⅰ)若a=
且函数f(x)的定义域为(-1,+∞),求函数f(x)的单调递增区间;
(Ⅱ)若a=0,求证f(x)≤|x+1|-1;
(Ⅲ)若函数y=f(x)的图象在原点O处的切线为l,试探究:是否存在实数a,使得函数y=f(x)的图象上存在点在直线l的上方?若存在,试求a的取值范围;若不存在,请说明理由.
(Ⅰ)若a=
| 2 |
| 3 |
(Ⅱ)若a=0,求证f(x)≤|x+1|-1;
(Ⅲ)若函数y=f(x)的图象在原点O处的切线为l,试探究:是否存在实数a,使得函数y=f(x)的图象上存在点在直线l的上方?若存在,试求a的取值范围;若不存在,请说明理由.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:综合题,导数的综合应用
分析:(Ⅰ)当a=
且x>-1时,f(x)=ln(x+1)-
x2,求导,在定义域内解不等式f′(x)>0可得;
(Ⅱ)当a=0时,不等式f(x)≤|x+1|-1即ln|x+1|-|x+1|+1≤0,令t=|x+1|,则t>0,此时不等式ln|x+1|-|x+1|+1≤0等价于不等式lnt-t+1≤0(t>0),令φ(t)=lnt-t+1,利用导数可证明φ(t)≤0;
(Ⅲ)由导数的几何意义可求得直线l的方程为y=x.令g(x)=ln|x+1|-ax2-x,则命题“函数y=f(x)的图象上存在点在直线l的上方”可等价转化为“存在x∈(-∞,-1)∪(-1,+∞),使得g(x)>0.”分①当a>0时,②a≤0两种情况讨论,a>0时可化为极大值大于0;a≤0时,由存在x=-e-1使得g(-e-1)=e+2-a(e+1)2>0恒成立.
| 2 |
| 3 |
| 2 |
| 3 |
(Ⅱ)当a=0时,不等式f(x)≤|x+1|-1即ln|x+1|-|x+1|+1≤0,令t=|x+1|,则t>0,此时不等式ln|x+1|-|x+1|+1≤0等价于不等式lnt-t+1≤0(t>0),令φ(t)=lnt-t+1,利用导数可证明φ(t)≤0;
(Ⅲ)由导数的几何意义可求得直线l的方程为y=x.令g(x)=ln|x+1|-ax2-x,则命题“函数y=f(x)的图象上存在点在直线l的上方”可等价转化为“存在x∈(-∞,-1)∪(-1,+∞),使得g(x)>0.”分①当a>0时,②a≤0两种情况讨论,a>0时可化为极大值大于0;a≤0时,由存在x=-e-1使得g(-e-1)=e+2-a(e+1)2>0恒成立.
解答:
解:(Ⅰ)当a=
且x>-1时,f(x)=ln(x+1)-
x2,
f′(x)=
-
x=
=-
,
令f′(x)>0,∵x>-1,∴(2x+3)(2x-1)<0,解得-1<x<
,
∴函数f(x)的单调递增区间为(-1,
);
(Ⅱ)当a=0时,f(x)=ln|x+1|,不等式f(x)≤|x+1|-1即ln|x+1|-|x+1|+1≤0,
令t=|x+1|,则t>0,
此时不等式ln|x+1|-|x+1|+1≤0等价于不等式lnt-t+1≤0(t>0),
令φ(t)=lnt-t+1,则φ′(t)=
-1=
.
令φ′(t)=0,得t=1,
当t∈(0,1)时φ′(t)>0,φ(t)递增;当t∈(1,+∞)时,φ′(t)<0,φ(t)递减,
故t=1时,φ(t)取得极大值,也为最大值,
∴t>0时,φ(t)≤φ(1)=0,即lnt-t+1≤0,
∴f(x)≤|x+1|-1成立.
(Ⅲ)当x>-1时,f(x)=ln(x+1)-ax2.f′(x)=
-2ax,
∴直线l的斜率k=f′(0)=1,
又f(0)=0,∴直线l的方程为y=x.
令g(x)=ln|x+1|-ax2-x,则命题“函数y=f(x)的图象上存在点在直线l的上方”可等价转化为“存在x∈(-∞,-1)∪(-1,+∞),使得g(x)>0.”
当x>-1时,g(x)=ln(x+1)-ax2-x,g′(x)=
-2ax-1,当x<-1时,g(x)=ln(-x-1)-ax2-x,g′(x)=
-2ax-1,
∴对x∈(-∞,-1)∪(-1,+∞),都有g′(x)=
=
.
令g′(x)=0,解得x=0或x=-
.
①当a>0时,-
<-1,当x∈(-∞,-1-
)∪(-1,0)时,g′(x)>0;当x∈(-1-
,-1)∪(0,+∞)时,g′(x)<0;
∴x=-1-
或0时,g(x)取得极大值,
又g(-1-
)=ln
+
-a,g(0)=0,
∴为使命题“存在x∈(-∞,-1)∪(-1,+∞),使得g(x)>0”成立,只需g(-1-
)=ln
+
-a>0,
令t=
,则g(-1-
)=lnt-
+
t,令h(t)=lnt-
+
t(t>0),
∵h′(t)=
+
+
>0,∴h(t)在(0,+∞)上为增函数,
又注意到h(1)=0,∴当且仅当t=
>1,即0<a<
时,h(t)>0,
故关于a的不等式ln
+
-a>0的解集为{a|0<a<
};
②当a≤0时,∵存在x=-e-1使得g(-e-1)=e+2-a(e+1)2>0恒成立.
∴总存在点(-e-1,1-a(e+1)2)在直线l的上方.
综合①②,可知a的取值范围为{a|a<
}.
| 2 |
| 3 |
| 2 |
| 3 |
f′(x)=
| 1 |
| x+1 |
| 4 |
| 3 |
| -4x2-4x+3 |
| 3(x+1) |
| (2x+3)(2x-1) |
| 3(x+1) |
令f′(x)>0,∵x>-1,∴(2x+3)(2x-1)<0,解得-1<x<
| 1 |
| 2 |
∴函数f(x)的单调递增区间为(-1,
| 1 |
| 2 |
(Ⅱ)当a=0时,f(x)=ln|x+1|,不等式f(x)≤|x+1|-1即ln|x+1|-|x+1|+1≤0,
令t=|x+1|,则t>0,
此时不等式ln|x+1|-|x+1|+1≤0等价于不等式lnt-t+1≤0(t>0),
令φ(t)=lnt-t+1,则φ′(t)=
| 1 |
| t |
| 1-t |
| t |
令φ′(t)=0,得t=1,
当t∈(0,1)时φ′(t)>0,φ(t)递增;当t∈(1,+∞)时,φ′(t)<0,φ(t)递减,
故t=1时,φ(t)取得极大值,也为最大值,
∴t>0时,φ(t)≤φ(1)=0,即lnt-t+1≤0,
∴f(x)≤|x+1|-1成立.
(Ⅲ)当x>-1时,f(x)=ln(x+1)-ax2.f′(x)=
| 1 |
| x+1 |
∴直线l的斜率k=f′(0)=1,
又f(0)=0,∴直线l的方程为y=x.
令g(x)=ln|x+1|-ax2-x,则命题“函数y=f(x)的图象上存在点在直线l的上方”可等价转化为“存在x∈(-∞,-1)∪(-1,+∞),使得g(x)>0.”
当x>-1时,g(x)=ln(x+1)-ax2-x,g′(x)=
| 1 |
| x+1 |
| 1 |
| x+1 |
∴对x∈(-∞,-1)∪(-1,+∞),都有g′(x)=
| -2ax2-(2a+1)x |
| x+1 |
-2ax(x+1+
| ||
| x+1 |
令g′(x)=0,解得x=0或x=-
| 2a+1 |
| 2a |
①当a>0时,-
| 2a+1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2a |
∴x=-1-
| 1 |
| 2a |
又g(-1-
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 4a |
∴为使命题“存在x∈(-∞,-1)∪(-1,+∞),使得g(x)>0”成立,只需g(-1-
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 4a |
令t=
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2t |
| 1 |
| 2 |
| 1 |
| 2t |
| 1 |
| 2 |
∵h′(t)=
| 1 |
| t |
| 1 |
| 2t2 |
| 1 |
| 2 |
又注意到h(1)=0,∴当且仅当t=
| 1 |
| 2a |
| 1 |
| 2 |
故关于a的不等式ln
| 1 |
| 2a |
| 1 |
| 4a |
| 1 |
| 2 |
②当a≤0时,∵存在x=-e-1使得g(-e-1)=e+2-a(e+1)2>0恒成立.
∴总存在点(-e-1,1-a(e+1)2)在直线l的上方.
综合①②,可知a的取值范围为{a|a<
| 1 |
| 2 |
点评:本题主要考查函数、导数等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、分类与整合思想、函数与方程思想、数形结合思想等.

练习册系列答案
相关题目
i是虚数单位,
的共轭复数为( )
| 2i |
| 1-i |
| A、-1+i | B、1+i |
| C、-1-i | D、1-i |
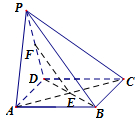 如图,已知四棱锥P-ABCD的底面为菱形,对角线AC与BD相交于点E,平面PAC垂直于底面ABCD,线段PD的中点为F.
如图,已知四棱锥P-ABCD的底面为菱形,对角线AC与BD相交于点E,平面PAC垂直于底面ABCD,线段PD的中点为F.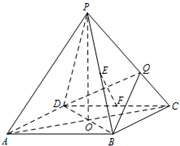 如图,正四棱锥P-ABCD的高为PO,PO=AB=2.E,F分别是棱PB,CD的中点,Q是棱PC上的点.
如图,正四棱锥P-ABCD的高为PO,PO=AB=2.E,F分别是棱PB,CD的中点,Q是棱PC上的点.