题目内容
数列{an}满足an=Sn-1+n，a1=0，求{an}的通项公式．
考点：数列递推式
专题：点列、递归数列与数学归纳法
分析：在数列递推式中取n=n+1得到另一递推式，作差后得到新的等比数列{an+1}，由等比数列的通项公式得答案．
解答：
解：由an=Sn-1+n（n≥2），得：
an+1=Sn+n+1，
两式作差得：an+1-an=an+1，
即an+1=2an+1，
an=2an-1+1．
则an+1=2（an-1+1）（n≥2）．
又a1+1=0+1=1≠0，
∴数列{an+1}是以1为首项，以2为公比的等比数列．
∴an+1=1×2n-1，
an=2n-1-1（n≥2）．
验证a1=0适合上式．
∴an=2n-1-1．
an+1=Sn+n+1，
两式作差得：an+1-an=an+1，
即an+1=2an+1，
an=2an-1+1．
则an+1=2（an-1+1）（n≥2）．
又a1+1=0+1=1≠0，
∴数列{an+1}是以1为首项，以2为公比的等比数列．
∴an+1=1×2n-1，
an=2n-1-1（n≥2）．
验证a1=0适合上式．
∴an=2n-1-1．
点评：本题考查数列递推式，考查了等比关系的确定，是中档题．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
设n∈N*，曲线y=xn（1-x）在x=2处的切线与y轴交点的纵坐标为an，则a4为（ ）
| A、80 | B、32 |
| C、192 | D、256 |
i是虚数单位，
的共轭复数为（ ）
| 2i |
| 1-i |
| A、-1+i | B、1+i |
| C、-1-i | D、1-i |
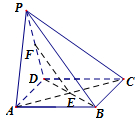如图，已知四棱锥P-ABCD的底面为菱形，对角线AC与BD相交于点E，平面PAC垂直于底面ABCD，线段PD的中点为F．