题目内容
已知函数g(x)=ax2-2ax+1+b(a>0)在区间[2,3]上的最大值为4,最小值为1,记f(x)=g(|x|).
(1)求实数a,b的值;
(2)若不等式f(log2k)>f(2)成立,求实数k的取值范围;
(3)对于任意满足p=x0<x1<x2<…<xn-1<xn=q(n∈N*,n≥3)的自变量x0,x1,x2,…,xn,如果存在一个常数M>0,使得定义在区间[p,q]上的一个函数m(x),|m(x1)-m(x0)|+|m(x2)-m(x1)|+…+|m(xn)-m(xn-1)|≤M恒成立,则称函数m(x)为区间[p,q]上的有界变差函数.试判断函数f(x)是否区间[1,3]上的有界变差函数,若是,求出M的最小值;若不是,请说明理由.
(1)求实数a,b的值;
(2)若不等式f(log2k)>f(2)成立,求实数k的取值范围;
(3)对于任意满足p=x0<x1<x2<…<xn-1<xn=q(n∈N*,n≥3)的自变量x0,x1,x2,…,xn,如果存在一个常数M>0,使得定义在区间[p,q]上的一个函数m(x),|m(x1)-m(x0)|+|m(x2)-m(x1)|+…+|m(xn)-m(xn-1)|≤M恒成立,则称函数m(x)为区间[p,q]上的有界变差函数.试判断函数f(x)是否区间[1,3]上的有界变差函数,若是,求出M的最小值;若不是,请说明理由.
考点:利用导数研究函数的单调性,二次函数在闭区间上的最值
专题:导数的综合应用
分析:(1)由g(x)的对称轴x=1得g(x)在区间[2,3]上是增函数,得方程组求出a,b即可;(2)由(1)求出f(x)的表达式,解不等式求出即可;(3)由f(x)的表达式得f(x)为[1,3]上的单调递增函数,根据有界变差函数的概念求出即可.
解答:
解:(1)∵g(x)=a(x-1)2+1+b-a,
又a>0,∴g(x)在区间[2,3]上是增函数,
故
,
解得:a=1,b=0.
(2)由(1)得:g(x)=x2-2x+1,
故f(x)=x2-2|x|+1是偶函数,
∴不等式f(
)>f(2)可化为|
|>2,
解得:k∈(0,
)∪(4,+∞).
(3)∵f(x)=
,
∴f(x)为[1,3]上的单调递增函数,
则对于任意满足1=x0<x1<x2<…<xn-1<xn=3(n∈N*,n≥3)的自变量x0,x1,x2,…,xn,
有f(1)=f(x0)<f(x1)<f(x2)<…<f(xn-1)<f(xn)=f(3),
∴|f(x1)-f(x0)|+|f(x2)-f(x1)|+…+|f(xn)-f(xn-1)|
=f(x1)-f(x0)+f(x2)-f(x1)+…+f(xn)-f(xn-1)
=f(xn)-f(xn-1)
=f(3)-f(1)
=4,
∴存在常数M≥4,使得
|m(x1)-m(x0)|+|m(x2)-m(x1)|+…+|m(xn)-m(xn-1)|≤M.
函数f(x)为区间[1,3]上的有界变差函数.即M的最小值为4.
又a>0,∴g(x)在区间[2,3]上是增函数,
故
|
解得:a=1,b=0.
(2)由(1)得:g(x)=x2-2x+1,
故f(x)=x2-2|x|+1是偶函数,
∴不等式f(
| log | k 2 |
| log | k 2 |
解得:k∈(0,
| 1 |
| 4 |
(3)∵f(x)=
|
∴f(x)为[1,3]上的单调递增函数,
则对于任意满足1=x0<x1<x2<…<xn-1<xn=3(n∈N*,n≥3)的自变量x0,x1,x2,…,xn,
有f(1)=f(x0)<f(x1)<f(x2)<…<f(xn-1)<f(xn)=f(3),
∴|f(x1)-f(x0)|+|f(x2)-f(x1)|+…+|f(xn)-f(xn-1)|
=f(x1)-f(x0)+f(x2)-f(x1)+…+f(xn)-f(xn-1)
=f(xn)-f(xn-1)
=f(3)-f(1)
=4,
∴存在常数M≥4,使得
|m(x1)-m(x0)|+|m(x2)-m(x1)|+…+|m(xn)-m(xn-1)|≤M.
函数f(x)为区间[1,3]上的有界变差函数.即M的最小值为4.
点评:本题考察了函数的性质,导数的应用,函数的单调性,新概念问题,是一道综合题.

练习册系列答案
相关题目
设a,b是两条不同直线,α,β是两个不同平面,下列四个命题中正确的是( )
| A、若a,b与α所成的角相等,则a∥b |
| B、若a∥α,b∥β,α∥β,则a∥b |
| C、若a⊥α,b⊥β,α⊥β,则a⊥b |
| D、若a?α,b?β,a∥b,则α∥β |
若实数x,y满足
,则z=2x+2y的最小值是( )
|
| A、0 | ||
| B、1 | ||
C、
| ||
| D、9 |
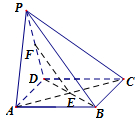 如图,已知四棱锥P-ABCD的底面为菱形,对角线AC与BD相交于点E,平面PAC垂直于底面ABCD,线段PD的中点为F.
如图,已知四棱锥P-ABCD的底面为菱形,对角线AC与BD相交于点E,平面PAC垂直于底面ABCD,线段PD的中点为F. 如图所示,在三棱锥P-ABC中,E、F分别为AC、BC的中点.
如图所示,在三棱锥P-ABC中,E、F分别为AC、BC的中点.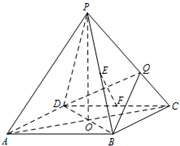 如图,正四棱锥P-ABCD的高为PO,PO=AB=2.E,F分别是棱PB,CD的中点,Q是棱PC上的点.
如图,正四棱锥P-ABCD的高为PO,PO=AB=2.E,F分别是棱PB,CD的中点,Q是棱PC上的点. 如图,△ABC内接于⊙O,AB=AC,点D在⊙O上,AD⊥AB,AD交BC于点E,点F在DA的延长线上,AF=AE,求证:
如图,△ABC内接于⊙O,AB=AC,点D在⊙O上,AD⊥AB,AD交BC于点E,点F在DA的延长线上,AF=AE,求证: