题目内容
用白铁皮做一个平底、圆锥形盖的圆柱形粮囤,粮囤容积为(8+8
)πm3(不含锥形盖内空间),盖子的母线与底面圆半径的夹角为45°,设粮囤的底面圆半径为Rm,需用白铁皮的面积记为S(R)m2(不计接头等).
(1)将S(R)表示为R的函数;
(2)求S(R)的最小值及对应的粮囤的总高度.(含圆锥顶盖)
| 2 |
(1)将S(R)表示为R的函数;
(2)求S(R)的最小值及对应的粮囤的总高度.(含圆锥顶盖)
考点:利用导数求闭区间上函数的最值,函数最值的应用,旋转体(圆柱、圆锥、圆台)
专题:函数的性质及应用,导数的综合应用
分析:(1)求需要的铁皮的面积,实际上是求圆柱体的表面积,又因圆柱的表面积=侧面积+底面积×2,代入数据即可求解;即可将S(R)表示为R的函数;
(2)求出S(R)的导数,利用导数值为0判断函数的最小值,即可求解粮囤的总高度.(含圆锥顶盖)
(2)求出S(R)的导数,利用导数值为0判断函数的最小值,即可求解粮囤的总高度.(含圆锥顶盖)
解答:
解:(1)S(R)=2πRh+πR2+
•2πR•
R=2πR•
+(1+
)πR2
=
+(1+
)πR2=
+(1+
)πR2(R>0)…(7分)
(2)S′(R)=-
+2(1+
)πR,
令S'(R)=0,得R=2…(10分)
当R>2时,S'(R)>0,
当R<2时S'(R)<0,
∴当R=2时,S(R)取得极小值也是最小值,且S(R)min=S(2)=8(1+
)π,…(13分)
此时圆柱的高为2(1+
),圆锥盖的高为
,
∴粮囤的总高度为(2+3
)m…(15分)
答:(1)
S(R)=
+(1+
)πR2;(2)S(R)min=S(2)=8(1+
)π,对应粮囤的总高度为(2+3
)m.…(16分).
| 1 |
| 2 |
| 2 |
| V |
| πR2 |
| 2 |
=
| 2V |
| R |
| 2 |
16(1+
| ||
| R |
| 2 |
(2)S′(R)=-
16(1+
| ||
| R2 |
| 2 |
令S'(R)=0,得R=2…(10分)
当R>2时,S'(R)>0,
当R<2时S'(R)<0,
∴当R=2时,S(R)取得极小值也是最小值,且S(R)min=S(2)=8(1+
| 2 |
此时圆柱的高为2(1+
| 2 |
| 2 |
∴粮囤的总高度为(2+3
| 2 |
答:(1)
| 2V |
| R |
16(1+
| ||
| R |
| 2 |
| 2 |
| 2 |
点评:此题主要考查圆柱体的表面积和体积的计算方法在实际生活中的应用.考查导数在函数的最值中的应用.

练习册系列答案
相关题目
二项式(2
-
)6的展开式的常数项是( )
| x |
| 1 | ||
2
|
| A、20 | B、-20 |
| C、15 | D、-15 |
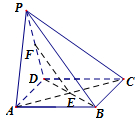 如图,已知四棱锥P-ABCD的底面为菱形,对角线AC与BD相交于点E,平面PAC垂直于底面ABCD,线段PD的中点为F.
如图,已知四棱锥P-ABCD的底面为菱形,对角线AC与BD相交于点E,平面PAC垂直于底面ABCD,线段PD的中点为F. 如图所示,在三棱锥P-ABC中,E、F分别为AC、BC的中点.
如图所示,在三棱锥P-ABC中,E、F分别为AC、BC的中点.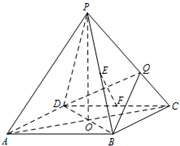 如图,正四棱锥P-ABCD的高为PO,PO=AB=2.E,F分别是棱PB,CD的中点,Q是棱PC上的点.
如图,正四棱锥P-ABCD的高为PO,PO=AB=2.E,F分别是棱PB,CD的中点,Q是棱PC上的点.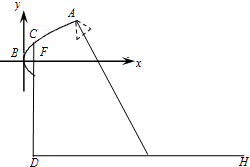 为了迎接青奥会,南京将在主干道统一安装某种新型节能路灯,该路灯由灯柱和支架组成.在如图所示的直角坐标系中,支架ACB是抛物线y2=2x的一部分,灯柱CD经过该抛物线的焦点F且与路面垂直,其中C在抛物线上,B为抛物线的顶点,DH表示道路路面,BF∥DH,A为锥形灯罩的顶,灯罩轴线与抛物线在A处的切线垂直.安装时要求锥形灯罩的顶到灯柱的距离是1.5米,灯罩的轴线正好通过道路路面的中线.
为了迎接青奥会,南京将在主干道统一安装某种新型节能路灯,该路灯由灯柱和支架组成.在如图所示的直角坐标系中,支架ACB是抛物线y2=2x的一部分,灯柱CD经过该抛物线的焦点F且与路面垂直,其中C在抛物线上,B为抛物线的顶点,DH表示道路路面,BF∥DH,A为锥形灯罩的顶,灯罩轴线与抛物线在A处的切线垂直.安装时要求锥形灯罩的顶到灯柱的距离是1.5米,灯罩的轴线正好通过道路路面的中线.