题目内容
2. 如图,D是直角△ABC斜边BC上一点,$AC=\sqrt{2}DC$.
如图,D是直角△ABC斜边BC上一点,$AC=\sqrt{2}DC$.(Ⅰ)若BD=2DC=2,求AD;
(Ⅱ)若AB=AD,求:sinB.
分析 (Ⅰ)由已知利用勾股定理可求AB,求得cosB,进而利用余弦定理可求AD的值.
(Ⅱ)在△ADC中,由正弦定理及已知可求$\frac{{\sqrt{2}DC}}{sinB}=\frac{DC}{sin(B-C)}$,又$B=\frac{π}{2}-C$,即可解得sinB的值.
解答 解:(Ⅰ)∵D是直角△ABC斜边BC上一点,$AC=\sqrt{2}DC$,BD=2DC=2,
∴AB=$\sqrt{B{C}^{2}-A{C}^{2}}$=$\sqrt{7}$,
∴cosB=$\frac{AB}{BC}$=$\frac{\sqrt{7}}{3}$,
∴AD=$\sqrt{A{B}^{2}+B{D}^{2}-2AB•AD•cosB}$=$\sqrt{7+4-2×\sqrt{7}×2×\frac{\sqrt{7}}{3}}$
=$\frac{\sqrt{15}}{3}$.
(Ⅱ)在△ADC中,$\frac{AC}{sin∠ADC}=\frac{DC}{sin∠CAD}$即$\frac{{\sqrt{2}DC}}{sinB}=\frac{DC}{sin(B-C)}$,
而$B=\frac{π}{2}-C$,
∴$\frac{{\sqrt{2}}}{sinB}=\frac{1}{{sin(2B-\frac{π}{2})}}$,
∴-$\sqrt{2}$cos2B=sinB,
∴$2\sqrt{2}si{n}^{2}B-sinB-\sqrt{2}$=0,
解得$sinB=\frac{{\sqrt{2}+\sqrt{34}}}{8}$.
点评 本题主要考查了勾股定理,余弦定理,正弦定理在解三角形中的应用,考查了转化思想和数形结合思想的应用,属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
11.设a是实数,且$\frac{2a}{1+i}$+1+i是实数,则a=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | -1 |
10.下列命题是真命题的为( )
| A. | 若$\frac{1}{x}$=$\frac{1}{y}$,则x=y | B. | 若x2≤4,则x=1 | C. | 若x=y,则$\sqrt{x}$=$\sqrt{y}$ | D. | 若x<y,则 x2<y2 |
17.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1与椭圆$\frac{x^2}{m^2}+\frac{y^2}{b^2}$=1(m>b>0)的离心率之积等于1,则以a,b,m为边长的三角形一定是( )
| A. | 等腰三角形 | B. | 钝角三角形 | C. | 锐角三角形 | D. | 直角三角形 |
14.有编号为D1,D2,…,D10的10个零件,测量其直径(单位:mm),得到下面数据:
其中直径在区间(148,152]内的零件为一等品.
(1)从上述10个零件中,随机抽取2个,求这2个零件均为一等品的概率;
(2)从一等品零件中,随机抽取2个.用ξ表示这2个零件直径之差的绝对值,求随机变量ξ的分布列及数学期望.
其中直径在区间(148,152]内的零件为一等品.
| 编号 | D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | D10 |
| 直径 | 151 | 148 | 149 | 151 | 149 | 152 | 147 | 146 | 153 | 148 |
(2)从一等品零件中,随机抽取2个.用ξ表示这2个零件直径之差的绝对值,求随机变量ξ的分布列及数学期望.
12.函数y=x2cosx的导数为( )
| A. | y′=x2cosx-2xsin x | B. | y′=2xcos x+x2sin x | ||
| C. | y′=2xcosx-x2sinx | D. | y′=xcosx-x2sin x |
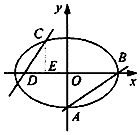 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$(a>b>0)的离心率$e=\frac{{\sqrt{6}}}{3}$,直线AB分别交椭圆下顶点A(0,-1)和右顶点B.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$(a>b>0)的离心率$e=\frac{{\sqrt{6}}}{3}$,直线AB分别交椭圆下顶点A(0,-1)和右顶点B.