题目内容
19.已知函数f(x)=$\left\{\begin{array}{l}12ax+1,0<x<a\\{log_{\frac{1}{2}}}x+2,a≤x<1\end{array}$且f(a2)=$\frac{5}{2}$,若当0<x1<x2<1时,f(x1)=f(x2),则x1•f(x2)的取值范围为( )| A. | $(\frac{1}{6},\frac{1}{3}]$ | B. | $(\frac{1}{3},1]$ | C. | $[\frac{1}{6},\frac{1}{3})$ | D. | $[\frac{1}{3},1)$ |
分析 先根据函数的解析式和f(a2)=$\frac{5}{2}$,求出a的值,再画出f(x)的图象,结合图象和f(x1)=f(x2),求出x1的范围和f(x2)的范围,问题得以解决.
解答 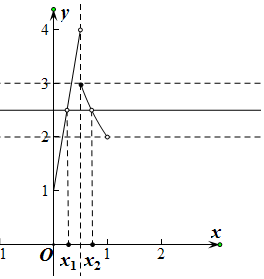 解:∵0<a<1,
解:∵0<a<1,
∴a2<a
∵f(a2)=$\frac{5}{2}$,
∴12a•a2+1=$\frac{5}{2}$
解得a=$\frac{1}{2}$,
∴f(x)=$\left\{\begin{array}{l}{6x+1,0<x<\frac{1}{2}}\\{lo{g}_{\frac{1}{2}}x+2,\frac{1}{2}≤x<1}\end{array}\right.$,
画出函数f(x)的图象,如图所示,
∵0<x1<x2<1时,f(x1)=f(x2),
∴当x=1时,f(1)=log${\;}_{\frac{1}{2}}$1+2=2,
∴6x+1=2,解得x=$\frac{1}{6}$,
当x=$\frac{1}{2}$时,f($\frac{1}{2}$)=log${\;}_{\frac{1}{2}}$$\frac{1}{2}$+2=3,
∴6x+1=3,解得x=$\frac{1}{3}$,
∴$\frac{1}{6}$<x1<≤$\frac{1}{3}$,2<f(x2)≤3,
∴$\frac{1}{3}$<x1•f(x2)≤1,
故选:B
点评 本题考查了分段函数和函数图象应用以及不等式的性质,关键是求出a的值,画出函数的图象,属于中档题

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
10.设M,N为两个随机事件,如果M,N为互斥事件($\overline{M}$,$\overline{N}$表示M,N的对立事件),那么( )
| A. | $\overline{M}$∪$\overline{N}$是必然事件 | B. | M∪N是必然事件 | ||
| C. | $\overline{M}$∩$\overline{N}$=∅ | D. | $\overline{M}$与$\overline{N}$一定不为互斥事件 |
14.如果有95%的把握说事件A和B有关,那么具体算出的数据满足( )
| A. | K 2>3.841 | B. | K 2<3.841 | C. | K 2>6.635 | D. | K 2<6.635 |
8.已知某产品的广告费用x与销售额y之间有如下的对应数据:
(1)y与x是否具有线性相关关系?若有,求出y对x的线性回归方程;
(2)据此估计广告费用为11万元时销售额的值.
(参考公式:$\stackrel{∧}{b}$=$\frac{{{\sum_{i=1}^{n}x}_{i}y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-{n\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
| x(万元) | 2 | 4 | 5 | 6 | 8 |
| y(万元) | 30 | 40 | 60 | 50 | 70 |
(2)据此估计广告费用为11万元时销售额的值.
(参考公式:$\stackrel{∧}{b}$=$\frac{{{\sum_{i=1}^{n}x}_{i}y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-{n\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
