题目内容
8.已知某产品的广告费用x与销售额y之间有如下的对应数据:| x(万元) | 2 | 4 | 5 | 6 | 8 |
| y(万元) | 30 | 40 | 60 | 50 | 70 |
(2)据此估计广告费用为11万元时销售额的值.
(参考公式:$\stackrel{∧}{b}$=$\frac{{{\sum_{i=1}^{n}x}_{i}y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-{n\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
分析 (1)根据所给的数据计算出x,y的平均数和回归直线的斜率,即可写出回归直线方程,
(2)由(1)中的回归直线方程,把所给的自变量x代入方程,得到y的一个估计值,得到结果.
解答 解:(1)y与x具有线性相关关系,$\overline{x}$=5,$\overline{y}$=50,(2分)
$\sum_{i=1}^{5}{{x}_{i}}^{2}$=145,$\sum_{i=1}^{5}{x}_{i}{y}_{i}$=2×30+4×40+5×60+6×50+8×70=1380,(4分)
∴$\stackrel{∧}{b}$=$\frac{{{\sum_{i=1}^{n}x}_{i}y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-{n\overline{x}}^{2}}$=6.5,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=17.5,(7分)
∴回归直线方程为y=6.5x+17.5.(8分)
(2)x=11时,预报y的值为y=11×6.5+17.5=89.
答:广告费用为11销售收入y的值大约89万元.(12分)
点评 本题考查回归分析的初步应用,写方程要用的斜率和x,y的平均数都要经过计算算出,这样的题有一定的运算量,是一个基础题.

练习册系列答案
相关题目
19.已知函数f(x)=$\left\{\begin{array}{l}12ax+1,0<x<a\\{log_{\frac{1}{2}}}x+2,a≤x<1\end{array}$且f(a2)=$\frac{5}{2}$,若当0<x1<x2<1时,f(x1)=f(x2),则x1•f(x2)的取值范围为( )
| A. | $(\frac{1}{6},\frac{1}{3}]$ | B. | $(\frac{1}{3},1]$ | C. | $[\frac{1}{6},\frac{1}{3})$ | D. | $[\frac{1}{3},1)$ |
3.若复数z满足$\frac{zi}{z-i}=1$,其中i为虚数单位,则复数z的共轭复数为( )
| A. | $-\frac{1}{2}+\frac{i}{2}$ | B. | $-\frac{1}{2}-\frac{i}{2}$ | C. | $\frac{1}{2}-\frac{i}{2}$ | D. | $\frac{1}{2}+\frac{i}{2}$ |
20.已知函数f(x)=x3-3x2+ax+2,曲线y=f(x)在点(0,2)处的切线与x轴交点的横坐标为-2,则a的值为( )
| A. | 1 | B. | 3 | C. | $\frac{1}{2}$ | D. | 5 |
17.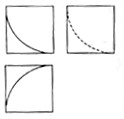 如图所示,某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1,圆心角为90°的圆弧,则该几何体的体积是( )
如图所示,某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1,圆心角为90°的圆弧,则该几何体的体积是( )
 如图所示,某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1,圆心角为90°的圆弧,则该几何体的体积是( )
如图所示,某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1,圆心角为90°的圆弧,则该几何体的体积是( )| A. | 1-$\frac{π}{12}$ | B. | 1-$\frac{π}{3}$ | C. | 1-$\frac{π}{6}$ | D. | 1-$\frac{π}{24}$ |
18.在2,0,1,7这组数据中,随机取出三个不同的数,则数字2是取出的三个不同数的中位数的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |