题目内容
4.已知α∈(0,$\frac{π}{2}$),β∈($\frac{π}{2}$,π)且$sin(α+β)=\frac{3}{5}$,$cosβ=-\frac{5}{13}$,求sinα的值.分析 构造思想,sinα=sin(α+β-β),利用和与差公式打开,根据$sin(α+β)=\frac{3}{5}$,$cosβ=-\frac{5}{13}$,求出cos(α+β),sinβ可得答案.
解答 解:由α∈(0,$\frac{π}{2}$),β∈($\frac{π}{2}$,π)∴α+β∈($\frac{π}{2},\frac{3π}{2}$),
又∵$sin(α+β)=\frac{3}{5}$>0,
∴α+β∈($\frac{π}{2}$,π),
则cos(α+β)=-$\frac{4}{5}$,
$cosβ=-\frac{5}{13}$,
则:sinβ=$\frac{12}{13}$.
那么:sinα=sin[(α+β)-β]=sin(α+β)cosβ-cos(α+β)sinβ=$\frac{3}{5}×(-\frac{5}{13})-$$(-\frac{4}{5})×\frac{12}{13}$=$\frac{33}{65}$
点评 本题主要考察了同角三角函数关系式和和与差公式的灵活应用,构造思想,属于基本知识的考查.

练习册系列答案
相关题目
19.已知函数f(x)=$\left\{\begin{array}{l}12ax+1,0<x<a\\{log_{\frac{1}{2}}}x+2,a≤x<1\end{array}$且f(a2)=$\frac{5}{2}$,若当0<x1<x2<1时,f(x1)=f(x2),则x1•f(x2)的取值范围为( )
| A. | $(\frac{1}{6},\frac{1}{3}]$ | B. | $(\frac{1}{3},1]$ | C. | $[\frac{1}{6},\frac{1}{3})$ | D. | $[\frac{1}{3},1)$ |
9.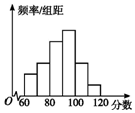 为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图,如图.已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[80,100)之间的学生人数是( )
为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图,如图.已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[80,100)之间的学生人数是( )
 为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图,如图.已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[80,100)之间的学生人数是( )
为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图,如图.已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在[80,100)之间的学生人数是( )| A. | 32 | B. | 27 | C. | 24 | D. | 33 |
14.若变量x,y满足条件$\left\{\begin{array}{l}x-y-1≤0\\ x+y-6≤0\\ x-3≥0\end{array}\right.$,则xy的取值范围是( )
| A. | [0,5] | B. | $[{5,\frac{35}{4}}]$ | C. | $[{0,\frac{35}{4}}]$ | D. | [6,9] |