题目内容
9.已知圆x2+y2=8内一点M(-1,2),AB为过点M且倾斜角为α的弦.(Ⅰ)当$α=\frac{3π}{4}$时,求AB的长;
(Ⅱ)当弦AB被点M平分时,求直线AB的方程.
分析 (Ⅰ)依题意直线AB的斜率为-1,可得直线AB的方程,根据圆心0(0,0)到直线AB的距离,由弦长公式求得AB的长.
(Ⅱ)当弦AB被点M平分时,OM⊥AB,故AB 的斜率为$\frac{1}{2}$,根据点斜式方程直线AB的方程.
解答 解:(Ⅰ) 当$α=\frac{3}{4}π$时,直线AB的方程为:y-2=-(x+1)⇒x+y-1=0
设圆心到直线AB的距离为d,则$d=\frac{{\sqrt{2}}}{2}$
∴$|{AB}|=2\sqrt{{r^2}-{d^2}}=\sqrt{30}$;
(Ⅱ)当弦AB被点M平分时,OM⊥AB.
因为KOM=-2,可得${K_{AB}}=\frac{1}{2}$,故直线AB的方程为:$y-2=\frac{1}{2}({x+1})$
即x-2y+5=0.
点评 本题考查用点斜式求直线方程,点到直线的距离公式,弦长公式的应用,求出圆心0(0,0)到直线AB的距离为d,是解题的关键.

练习册系列答案
相关题目
19.已知函数f(x)=$\left\{\begin{array}{l}12ax+1,0<x<a\\{log_{\frac{1}{2}}}x+2,a≤x<1\end{array}$且f(a2)=$\frac{5}{2}$,若当0<x1<x2<1时,f(x1)=f(x2),则x1•f(x2)的取值范围为( )
| A. | $(\frac{1}{6},\frac{1}{3}]$ | B. | $(\frac{1}{3},1]$ | C. | $[\frac{1}{6},\frac{1}{3})$ | D. | $[\frac{1}{3},1)$ |
20.已知函数f(x)=x3-3x2+ax+2,曲线y=f(x)在点(0,2)处的切线与x轴交点的横坐标为-2,则a的值为( )
| A. | 1 | B. | 3 | C. | $\frac{1}{2}$ | D. | 5 |
17.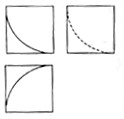 如图所示,某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1,圆心角为90°的圆弧,则该几何体的体积是( )
如图所示,某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1,圆心角为90°的圆弧,则该几何体的体积是( )
 如图所示,某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1,圆心角为90°的圆弧,则该几何体的体积是( )
如图所示,某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1,圆心角为90°的圆弧,则该几何体的体积是( )| A. | 1-$\frac{π}{12}$ | B. | 1-$\frac{π}{3}$ | C. | 1-$\frac{π}{6}$ | D. | 1-$\frac{π}{24}$ |
4.执行如图所示的程序框图,如果输入的a,b分别为56,140,则输出的a=( )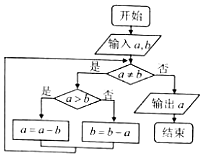

| A. | 0 | B. | 7 | C. | 14 | D. | 28 |
14.若变量x,y满足条件$\left\{\begin{array}{l}x-y-1≤0\\ x+y-6≤0\\ x-3≥0\end{array}\right.$,则xy的取值范围是( )
| A. | [0,5] | B. | $[{5,\frac{35}{4}}]$ | C. | $[{0,\frac{35}{4}}]$ | D. | [6,9] |
18.在2,0,1,7这组数据中,随机取出三个不同的数,则数字2是取出的三个不同数的中位数的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
