设F1.F2是椭圆$C:\frac{x^2}{5}+{y^2}=1$的两焦点.点P(异于点F1.F2)关于点F1.F2的对称点分别为点P1.P2.线段PQ的中点在椭圆C上.则|P1Q|+|P2Q|=4$\sqrt{5}$．题目和参考答案——青夏教育精英家教网—

题目内容

4．设F₁，F₂是椭圆$C：\frac{x^2}{5}+{y^2}=1$的两焦点，点P（异于点F₁，F₂）关于点F₁，F₂的对称点分别为点P₁，P₂，线段PQ的中点在椭圆C上，则|P₁Q|+|P₂Q|=4$\sqrt{5}$．

分析由题意作图象，设线段PQ的中点为M，连结MF₁，MF₂，从而可得|QP₁|=2|MF₁|，|QP₂|=2|MF₂|，从而结合椭圆的定义解得．

解答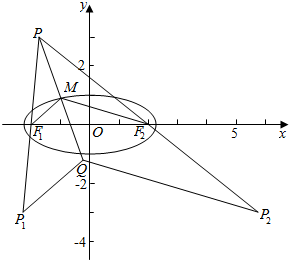解：由题意作图象如右图，
设线段PQ的中点为M，
连结MF₁，MF₂，
∵F₁是PP₁的中点，线段PQ的中点为M，
∴|QP₁|=2|MF₁|，
同理可得，
|QP₂|=2|MF₂|，
∴|P₁Q|+|P₂Q|=2（|MF₁|+|MF₂|）
=2•2a=4a，
∵a=$\sqrt{5}$，
∴4a=4$\sqrt{5}$；
故|P₁Q|+|P₂Q|=4$\sqrt{5}$；
故答案为：4$\sqrt{5}$．

点评本题考查了数形结合的思想应用及椭圆的定义的应用．

练习册系列答案

创新设计高考总复习系列答案

魔法教程课本诠释与思维拓展训练系列答案

15．若函数f（x）是定义在R上的偶函数，且当x≤0时，f（x）=x²+2x．
（1）写出函数f（x）（x∈R）的解析式．
（2）若函数g（x）=f（x）-2（a-1）x+2（x∈[1，2]），求函数g（x）的最小值．

12．命题“若x，y都是偶数，则x+y是偶数”的逆否命题是（　　）

	A．	若x，y不都是偶数，则x+y不是偶数		B．	若x，y都是偶数，则x+y不是偶数
	C．	若x+y是偶数，则x，y都是偶数		D．	若x+y不是偶数，则x，y不都是偶数

19．从1，2，3，4，5，6，7，8，9中任取七个不同的数，则这七个数的平均数是5的概率为（　　）

9．如图所示，某几何体的三视图，则该几何体的体积为（　　）