题目内容
19.从1,2,3,4,5,6,7,8,9中任取七个不同的数,则这七个数的平均数是5的概率为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{8}$ |
分析 先求出从1,2,3,4,5,6,7,8,9中任取七个不同的数的基本事件总数,再用列举法求出这七个数的平均数是5包含的基本事件的个数,由此能求出这七个数的平均数是5的概率.
解答 解:从1,2,3,4,5,6,7,8,9中任取七个不同的数,
基本事件总数n=${C}_{9}^{7}$=36,
这七个数的平均数是5包含的基本事件有:(2,3,4,5,6,7,8),
(1,3,4,5,6,7,9),(1,2,4,5,6,8,9),(1,2,3,5,7,8,9),共4个,
∴这七个数的平均数是5的概率为p=$\frac{4}{36}=\frac{1}{9}$.
故选:C.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.设集合M={x|0≤x<2},N={x|x-3<0},则M∩N=( )
| A. | {x|0≤x<1} | B. | {x|0≤x≤1} | C. | {x|0≤x<2} | D. | {x|0≤x≤2} |
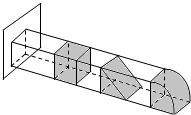 如图所示的三个几何体,一个是长方体,一个是直三棱柱,一个是过圆柱上、下底面圆心切下圆柱的四分之一部分,若这三个几何体的正视图和俯视图是相同的正方形,求他们的表面积之比.
如图所示的三个几何体,一个是长方体,一个是直三棱柱,一个是过圆柱上、下底面圆心切下圆柱的四分之一部分,若这三个几何体的正视图和俯视图是相同的正方形,求他们的表面积之比.