题目内容
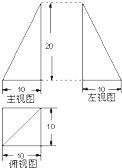某师傅用铁皮制作一封闭的工件，其三视图如图所示（单位长度：cm，图中水平线与竖线垂直），则制作该工件用去的铁皮的面积为（制作过程铁皮的损耗和厚度忽略不计）（ ）A、100（3+
| ||
B、200（3+
| ||
C、300（3+
| ||
| D、300cm2 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：本题以实际应用题为背景考查立体几何中的三视图．由三视图可知，该几何体的形状如图，它是底面为正方形，各个侧面均为直角三角形[的四棱锥，用去的铁皮的面积即该棱锥的表面积
解答：
解：由三视图可知，该几何体的形状如图，它是底面为正方形，各个侧面均为直角三角形的四棱锥，用去的铁皮的面积即该棱锥的表面积，其底面边长为10，故底面面积为10×10=100，
与底面垂直的两个侧面是全等的直角，两直角连年长度分别为10，20，故它们的面积皆为100，
另两个侧面也是全等的直角三角形，两直角边中一边是底面正方形的边长10，另一边可在与底面垂直的直角三角形中求得，其长为
=10
，
故此两侧面的面积皆为50
，
故此四棱锥的表面积为S=100（3+
）cm2．
故选：A
与底面垂直的两个侧面是全等的直角，两直角连年长度分别为10，20，故它们的面积皆为100，
另两个侧面也是全等的直角三角形，两直角边中一边是底面正方形的边长10，另一边可在与底面垂直的直角三角形中求得，其长为
| 102+202 |
| 5 |
故此两侧面的面积皆为50
| 5 |
故此四棱锥的表面积为S=100（3+
| 5 |
故选：A
点评：考点是由三视图求几何体的面积、体积，考查对三视图的理解与应用，主要考查三视图与实物图之间的关系，用三视图中的数据还原出实物图的数据，再根据相关的公式求表面积与体积，本题求的是表面积．三视图的投影规则是主视、俯视 长对正；主视、左视高平齐，左视、俯视 宽相等，本题以实际应用题为背景考查立体几何中的三视图．三视图是新课标的新增内容，在以后的高考中有加强的力度．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
设集合A={x|x2-2x≤0，x∈R}，B={y|y=-x2，-1≤x≤2}，则∁R（A∩B）等于（ ）
| A、R | B、{x|x∈R，x≠0} |
| C、{0} | D、φ |
已知a＞0，b＞0，a+b=1，则
+
的最大值为（ ）
| a+1 |
| b+1 |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
如果四棱锥的四条侧棱都相等，就称它为“等腰四棱锥”，四条侧棱称为它的腰，以下4个命题中，假命题是（ ）
| A、等腰四棱锥的腰与底面所成的角都相等 |
| B、等腰四棱锥的底面四边形必存在外接圆 |
| C、等腰四棱锥的侧面与底面所成的二面角都相等或互补 |
| D、等腰四棱锥的各顶点必在同一球面上 |
复数z=
，则（ ）
| 1-3i |
| 1+2i |
| A、|z|=2 |
| B、z的实部为1 |
| C、z的虚部为-i |
| D、z的共轭复数为-1+i |
若函数g（x）=log3（ax2+2x-1）有最大值1，则实数a的值等于（ ）
A、-
| ||
B、
| ||
C、-
| ||
| D、4 |