题目内容
若函数g(x)=log3(ax2+2x-1)有最大值1,则实数a的值等于( )
A、-
| ||
B、
| ||
C、-
| ||
| D、4 |
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:根据y=log3x的单调性,可得函数g(x)=log3(ax2+2x-1)有最大值1,则ax2+2x-1有最大值3,结合二次函数的图象和性质,可得a值.
解答:
解:∵函数g(x)=log3(ax2+2x-1)有最大值1,
故ax2+2x-1有最大值3,
即
=3,
解得:a=-
,
故选:C
故ax2+2x-1有最大值3,
即
| -4a-4 |
| 4a |
解得:a=-
| 1 |
| 4 |
故选:C
点评:本题考查的知识点是对数函数图象与性质,二次函数图象与性质,难度不大,属于基础题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
某报社做了一次关于“什么是新时代的雷锋精神”的调查,在A,B,C,D四个单位回收的问卷数依次成等差数列,且共回收1 000份,因报道需要,再从回收的问卷中按单位分层抽取容量为150的样本,若在B单位抽取30份,则在D单位抽取的问卷份( )
| A、60 | B、200 |
| C、400 | D、140 |
抛掷一颗骰子的点数为a,得到函数f(x)=sin
x,则y=f(x)在[0,a]上至少有5个零点的概率是( )
| aπ |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示的程序是用来( )


| A、计算3×10的值 |
| B、计算39值 |
| C、计算310的值 |
| D、计算1×2×3×…×10的值 |
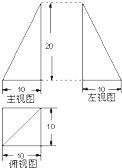 某师傅用铁皮制作一封闭的工件,其三视图如图所示(单位长度:cm,图中水平线与竖线垂直),则制作该工件用去的铁皮的面积为(制作过程铁皮的损耗和厚度忽略不计)( )
某师傅用铁皮制作一封闭的工件,其三视图如图所示(单位长度:cm,图中水平线与竖线垂直),则制作该工件用去的铁皮的面积为(制作过程铁皮的损耗和厚度忽略不计)( )A、100(3+
| ||
B、200(3+
| ||
C、300(3+
| ||
| D、300cm2 |