题目内容
已知函数f(x)在R上有意义,且满足:(1)f(x)是偶函数;(2)f(3)=999;(3)g(x)=f(x-1)是奇函数,求f(2015).
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:由f(x-1)是奇函数、f(x)是偶函数,可得f(x)=f(4+x),从而求得f(2015)=f(3),即可得到答案.
解答:
解:∵g(x)=f(x-1)是奇函数,故有f(-x-1)=-f(x-1),即f(-x-1)+f(x-1)=0
又∵f(x)是偶函数,得f(-x-1)=f(x+1),
∴f(x+1)+f(x-1)=0,用x+2代替x,得f(x+3)+f(x+1)=0,
两式对照,可得f(x+3)=f(x-1),即f[(x-1)+4]=f(x-1),
∴f(x+4)=f(x)对任意x∈R恒成立,可得f(x)的最小正周期为4,
∴f(2015)=f(3)=999.
又∵f(x)是偶函数,得f(-x-1)=f(x+1),
∴f(x+1)+f(x-1)=0,用x+2代替x,得f(x+3)+f(x+1)=0,
两式对照,可得f(x+3)=f(x-1),即f[(x-1)+4]=f(x-1),
∴f(x+4)=f(x)对任意x∈R恒成立,可得f(x)的最小正周期为4,
∴f(2015)=f(3)=999.
点评:本题综合考查抽象的函数奇偶性、周期性的应用,属于基础题.

练习册系列答案
相关题目
正三棱锥的高为1,底面边长为2
,内有一个球与四个面都相切,则棱锥的内切球的半径为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
定义在R上的函数f(x)满足:f(-x)=-f(x),f(x+1)=
,当x∈(-1,0)时,f(x)=2x-1,则f(log220)=( )
| 1 |
| f(x) |
A、-
| ||
B、-
| ||
C、
| ||
D、-
|
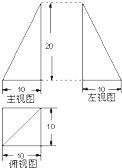 某师傅用铁皮制作一封闭的工件,其三视图如图所示(单位长度:cm,图中水平线与竖线垂直),则制作该工件用去的铁皮的面积为(制作过程铁皮的损耗和厚度忽略不计)( )
某师傅用铁皮制作一封闭的工件,其三视图如图所示(单位长度:cm,图中水平线与竖线垂直),则制作该工件用去的铁皮的面积为(制作过程铁皮的损耗和厚度忽略不计)( )A、100(3+
| ||
B、200(3+
| ||
C、300(3+
| ||
| D、300cm2 |
已知全集U=R,A={x|-1<x≤1},B={x|lg(2x2-1)≤0},则A∩(∁UB)等于( )
A、[
| ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|