题目内容
如果四棱锥的四条侧棱都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰,以下4个命题中,假命题是( )
| A、等腰四棱锥的腰与底面所成的角都相等 |
| B、等腰四棱锥的底面四边形必存在外接圆 |
| C、等腰四棱锥的侧面与底面所成的二面角都相等或互补 |
| D、等腰四棱锥的各顶点必在同一球面上 |
考点:命题的真假判断与应用
专题:空间角
分析:画出图形,根据条件,结合棱锥的侧棱与底面所成的角、二面角的平面角等知识,逐一判定即可.
解答:
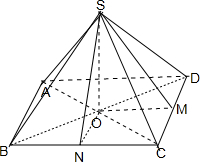 解:如图,
解:如图,
A:作SO⊥底面ABCD,∵SA=SB=SC=SD,∴∠SAO=∠SBO=∠SCO=∠SDO,即等腰四棱锥腰与底面所成的角相等,正确;
B:如图,由SA=SB=SC=SD得OA=OB=OC=OD,即等腰四棱锥的底面四边形存在外接圆,正确;
C:等腰四棱锥的侧面与底面所成的二面角相等或互补不一定成立,如图,OM⊥BD,ON⊥BC,∠SMO与∠SNO均为侧面与底面所成的二面角,但OM与ON不一定相等,故错误;
D:因为是等腰四棱锥,由B知,OA=OB=OC=OD,等腰四棱锥的外接球球心在棱锥的高所在直线上,故等腰四棱锥各顶点在同一个球面上,正确.
故选:C.
 解:如图,
解:如图,A:作SO⊥底面ABCD,∵SA=SB=SC=SD,∴∠SAO=∠SBO=∠SCO=∠SDO,即等腰四棱锥腰与底面所成的角相等,正确;
B:如图,由SA=SB=SC=SD得OA=OB=OC=OD,即等腰四棱锥的底面四边形存在外接圆,正确;
C:等腰四棱锥的侧面与底面所成的二面角相等或互补不一定成立,如图,OM⊥BD,ON⊥BC,∠SMO与∠SNO均为侧面与底面所成的二面角,但OM与ON不一定相等,故错误;
D:因为是等腰四棱锥,由B知,OA=OB=OC=OD,等腰四棱锥的外接球球心在棱锥的高所在直线上,故等腰四棱锥各顶点在同一个球面上,正确.
故选:C.
点评:本题考查棱锥的结构特征,着重考查侧棱与底面所成的角、二面角等概念,考查作图与空间想象能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
a=log
3,b=log
2,c=(
)0.3,则( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、a<b<c |
| B、a<c<b |
| C、b<c<a |
| D、b<a<c |
阅读程序框图,运行相应的程序,则输出i的值为( )


| A、3 | B、4 | C、5 | D、6 |
抛掷一颗骰子的点数为a,得到函数f(x)=sin
x,则y=f(x)在[0,a]上至少有5个零点的概率是( )
| aπ |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
定义在R上的函数f(x)满足:f(-x)=-f(x),f(x+1)=
,当x∈(-1,0)时,f(x)=2x-1,则f(log220)=( )
| 1 |
| f(x) |
A、-
| ||
B、-
| ||
C、
| ||
D、-
|
如图所示的程序是用来( )


| A、计算3×10的值 |
| B、计算39值 |
| C、计算310的值 |
| D、计算1×2×3×…×10的值 |
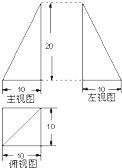 某师傅用铁皮制作一封闭的工件,其三视图如图所示(单位长度:cm,图中水平线与竖线垂直),则制作该工件用去的铁皮的面积为(制作过程铁皮的损耗和厚度忽略不计)( )
某师傅用铁皮制作一封闭的工件,其三视图如图所示(单位长度:cm,图中水平线与竖线垂直),则制作该工件用去的铁皮的面积为(制作过程铁皮的损耗和厚度忽略不计)( )A、100(3+
| ||
B、200(3+
| ||
C、300(3+
| ||
| D、300cm2 |