题目内容
已知a＞0，b＞0，a+b=1，则
+
的最大值为（ ）
| a+1 |
| b+1 |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
考点：函数的最值及其几何意义
专题：不等式的解法及应用
分析：根据基本不等式和条件先求出ab的范围，再将所求的式子进行平方后，利用ab的范围求出它的最大值．
解答：
解：∵a＞0，b＞0，且a+b=1，
∴a+b≥2
，解得ab≤
（当且仅当a=b时取等号），
则(
+
)2=a+b+2+2
=3+2
=3+2
≤3+2
=6（当且仅当a=b时取等号），
即
+
的最大值为：
，
故选：A．
∴a+b≥2
| ab |
| 1 |
| 4 |
则(
| a+1 |
| b+1 |
| (a+1)(b+1) |
=3+2
| ab+a+b+1 |
=3+2
| ab+2 |
|
即
| a+1 |
| b+1 |
| 6 |
故选：A．
点评：本题考查利用基本不等式求最值，体现了基本不等式的应用和转化的数学思想，注意等号成立的条件是否成立．
练习册系列答案
相关题目
设集合A={x|-x2+4x-3＞0}，B={x||2x-1|＞3}，则A∩B=（ ）
| A、{x|x＜-1或x＞1} |
| B、{x|x＜-1或x＞2} |
| C、{x|2＜x＜3} |
| D、R |
正三棱锥的高为1，底面边长为2
，内有一个球与四个面都相切，则棱锥的内切球的半径为（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
阅读程序框图，运行相应的程序，则输出i的值为（ ）
| A、3 | B、4 | C、5 | D、6 |
已知向量|
|=1，|
|=2，＜
，
＞=
，则|
+
|为（ ）
| a |
| b |
| a |
| b |
| π |
| 3 |
| a |
| b |
| A、9 | ||
| B、7 | ||
| C、3 | ||
D、
|
抛掷一颗骰子的点数为a，得到函数f（x）=sin
x，则y=f（x）在[0，a]上至少有5个零点的概率是（ ）
| aπ |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
定义在R上的函数f（x）满足：f（-x）=-f（x），f（x+1）=
，当x∈（-1，0）时，f（x）=2x-1，则f（log220）=（ ）
| 1 |
| f(x) |
A、-
| ||
B、-
| ||
C、
| ||
D、-
|
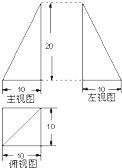某师傅用铁皮制作一封闭的工件，其三视图如图所示（单位长度：cm，图中水平线与竖线垂直），则制作该工件用去的铁皮的面积为（制作过程铁皮的损耗和厚度忽略不计）（ ）A、100（3+
| ||
B、200（3+
| ||
C、300（3+
| ||
| D、300cm2 |