题目内容
若集合A=（a，
，1）又可表示为{a2，a+b，0}，求a2014+b2013的值．
| b |
| a |
考点：集合的相等
专题：集合
分析：先求出a，b的值，再将a，b代入a2014+b2013，从而求出答案．
解答：
解：∵a≠0，∴
=0，∴b=0，∴a=-1，
∴a2014+b2013=（-1）2014+02013=1．
| b |
| a |
∴a2014+b2013=（-1）2014+02013=1．
点评：本题考查了集合的相等问题，考查集合的含义，是一道基础题．
练习册系列答案
智慧小复习系列答案
相关题目
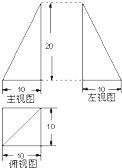某师傅用铁皮制作一封闭的工件，其三视图如图所示（单位长度：cm，图中水平线与竖线垂直），则制作该工件用去的铁皮的面积为（制作过程铁皮的损耗和厚度忽略不计）（ ）A、100（3+
| ||
B、200（3+
| ||
C、300（3+
| ||
| D、300cm2 |